题目内容
17. 如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是
如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.
(1)证明:AE⊥B1D;
(2)求二面角F-AC-B1的余弦值.
分析 (1)作辅助线利用线面垂直证明AE⊥B1D;
(2)建立合理的坐标系求出坐标利用两个面的法向量求得余弦值
解答 (1)证明:取AE的中点M,连接MB1,MD,则AE⊥MB1,AE⊥MD,所以AE⊥面MDB1,则AE⊥B1D--------------------(4分)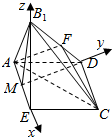
(2)解:分别以ME,MD,MB1为x,y,z轴建立空间直角坐标系,则$E(\frac{a}{2},0,0)$,$C(a,\frac{{\sqrt{3}}}{2}a,0)$$A(-\frac{a}{2},0,0)$,$D(0,\frac{{\sqrt{3}}}{2}a,0)$,${B_1}(0,0,\frac{{\sqrt{3}}}{2}a)$,$F({0,\frac{{\sqrt{3}}}{4}a,\frac{{\sqrt{3}}}{4}a})$,$\overrightarrow{AF}=({\frac{a}{2},\frac{{\sqrt{3}a}}{4},\frac{{\sqrt{3}a}}{4}}),\overrightarrow{AC}=({\frac{3a}{2},\frac{{\sqrt{3}}}{2}a,0}),\overrightarrow{A{B_1}}=({\frac{a}{2},0,\frac{{\sqrt{3}a}}{2}})$,
设面ACF的法向量为$\overrightarrow u=(x,y,z)$,
由$\left\{\begin{array}{l}\overrightarrow u•\overrightarrow{AC}=0\\ \overrightarrow u•\overrightarrow{AF}=0\end{array}\right.$有$\left\{\begin{array}{l}\frac{3}{2}ax+\frac{{\sqrt{3}}}{2}ay=0\\ \frac{a}{2}x+\frac{{\sqrt{3}a}}{4}y+\frac{{\sqrt{3}a}}{4}z=0\end{array}\right.$令x=1$\overrightarrow{u}=(1,-\sqrt{3},\frac{\sqrt{3}}{3})$-------(7分)
设B1AC的法向量$\overrightarrow{v}=({x}_{2},{y}_{2},{z}_{2})$,$\left\{\begin{array}{l}{\overrightarrow{u}•\overrightarrow{AC}=\overrightarrow{0}}\\{\overrightarrow{u}•\overrightarrow{A{B}_{1}}=\overrightarrow{0}}\end{array}\right.$有$\left\{\begin{array}{l}\frac{3a}{2}{x_2}+\frac{{\sqrt{3}a}}{2}{y_2}=0\\ \frac{a}{2}{x_2}+\frac{{\sqrt{3}a}}{2}{z_2}=0\end{array}\right.$令x2=1,$\overrightarrow v=(1,-\sqrt{3},-\frac{{\sqrt{3}}}{3})$,--------------------------------(9分)
所以$cos<\overrightarrow u,\overrightarrow v>=\frac{{1+3-\frac{1}{3}}}{{\sqrt{1+3+\frac{1}{3}}×\sqrt{1+3+\frac{1}{3}}}}=\frac{11}{13}$,
二面角F-AC-B1为锐角,故二面角F-AC-B1的余弦值为$\frac{11}{13}$.-------------(12分)
点评 本题考查利用线面垂直的性质定理证明线线垂直的方法和利用建立坐标系求得二面角的余弦值,属中档题,高考常考题型.

 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案| A. | 432 | B. | 288 | C. | 216 | D. | 144 |
| A. | (0,3) | B. | [2,3) | C. | (2,3) | D. | [3,+∞) |
| A. | -3 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
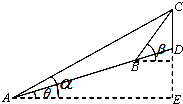 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.