题目内容
14．已知|z1|=1，z2∈Z，求证|$\frac{{z}_{1}-{z}_{2}}{1-\overline{{z}_{1}}•{z}_{2}}$|=1．分析 利用分析法直接证明所证明的等式．
解答 证明：要证明|$\frac{{z}_{1}-{z}_{2}}{1-\overline{{z}_{1}}•{z}_{2}}$|=1．即证明$|{z}_{1}-{z}_{2}|=|1-\overline{{z}_{1}}•{z}_{2}|$，即证明${（{|z}_{1}-{z}_{2}|）}^{2}={（\right|1-\overline{{z}_{1}}•{z}_{2}\left|）}^{2}$，可得$|{z}_{1}{|}^{2}-2|{z}_{1}\left|\right|{z}_{2}|+|{z}_{2}{|}^{2}=1-2\left|{z}_{2}\right|\left|\overline{{z}_{1}}\right|+\left|\overline{{z}_{1}}{|}^{2}\right|{z}_{2}{|}^{2}$，$-2|{z}_{1}\left|\right|{z}_{2}|+|{z}_{2}{|}^{2}=-2\left|{z}_{2}\right|\left|\overline{{z}_{1}}\right|+\left|\overline{{z}_{1}}{|}^{2}\right|{z}_{2}{|}^{2}$，
设z1=a+bi，|z1|=1，即证：$2|{z}_{1}\left|\right|{z}_{2}|=2|{z}_{2}\left|\right|\overline{{z}_{1}}|$，∵$|{z}_{1}|=|\overline{{z}_{1}}|$，
∴原式成立．
点评 本题考查复数的模，分析法的应用，考查逻辑推理能力．
练习册系列答案
相关题目
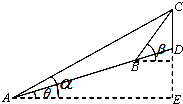如图，一山顶有一信号塔CD（CD所在的直线与地平面垂直），在山脚A处测得塔尖C的仰角为α，沿倾斜角为θ的山坡向上前进l米后到达B处，测得C的仰角为β．