题目内容
(本小题满分12分)
设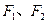 分别为椭圆
分别为椭圆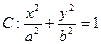 (
(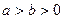 )的左、右焦点,过F2的
)的左、右焦点,过F2的
直线l与椭圆C相交于A、B两点,直线l的倾斜角为600,F1到直线l的
距离为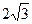 .
.
⑴求椭圆C的焦距;
⑵如果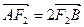 ,求椭圆C的方程.
,求椭圆C的方程.
设
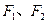 分别为椭圆
分别为椭圆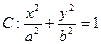 (
(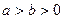 )的左、右焦点,过F2的
)的左、右焦点,过F2的直线l与椭圆C相交于A、B两点,直线l的倾斜角为600,F1到直线l的
距离为
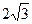 .
.⑴求椭圆C的焦距;
⑵如果
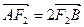 ,求椭圆C的方程.
,求椭圆C的方程.(1)4
(2)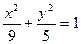 .
.
(2)
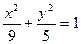 .
. 略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
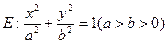 的左、右焦点分别为
的左、右焦点分别为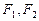 ,点
,点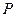 是
是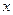 轴上方椭圆
轴上方椭圆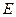 上的一点,且
上的一点,且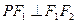 ,
, 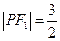 ,
, 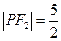 .
.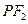 为直径的圆与以椭圆
为直径的圆与以椭圆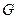 是椭圆
是椭圆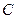 :
: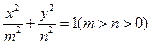 上的任意一点,
上的任意一点,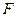 是椭圆
是椭圆 为直径的圆与以椭圆
为直径的圆与以椭圆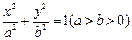 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.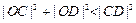 成立,求实数
成立,求实数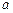 的取值范围.
的取值范围.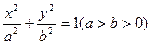 的离心率是
的离心率是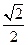 ,右焦点
,右焦点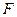 到上顶点的距离为
到上顶点的距离为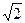 ,点
,点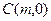 是线段
是线段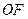 上的一个动点.
上的一个动点.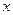 轴不垂直的直线
轴不垂直的直线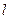 与椭圆交于
与椭圆交于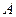 、
、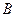 两点,使得
两点,使得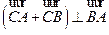 ,并说明理由.
,并说明理由.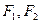 分别为椭圆
分别为椭圆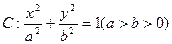 的左、右两个焦点.
的左、右两个焦点.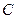 上的点
上的点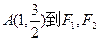 两点的距离之和等于4,
两点的距离之和等于4,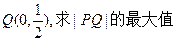 。
。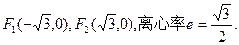
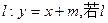 与此椭圆相交于不同的两点,求m的取值范围.
与此椭圆相交于不同的两点,求m的取值范围.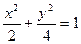 与射线y=
与射线y=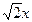 (x
(x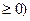 交于点A,过A作倾斜角互补的两条直线,
交于点A,过A作倾斜角互补的两条直线, 已知
已知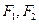 是椭圆
是椭圆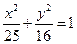 的两个焦点,P是椭圆上的一点,若
的两个焦点,P是椭圆上的一点,若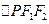 的内切圆半径为1,则点P到x轴的距离为( )
的内切圆半径为1,则点P到x轴的距离为( )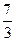

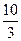
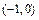 、B
、B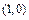 ,以AB为一腰作使∠DAB=
,以AB为一腰作使∠DAB=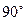 直角梯形ABCD,且
直角梯形ABCD,且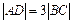 ,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为
,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为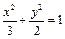 B.
B.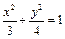 C.
C.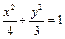 D.
D.