题目内容
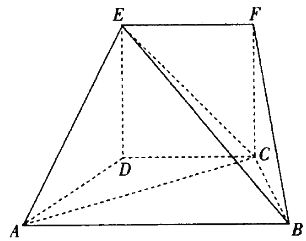
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
【答案】(1)![]()
![]() ;(2)
;(2)![]() 时,所用材料的总长度最小,最小值为
时,所用材料的总长度最小,最小值为![]() .
.
【解析】
(1)分别在△ABC和△ACD中,利用正弦定理即可解出答案;
(2)在△ABC中,利用正弦定理求出BC,再利用(1)的结果和三角函数的和差公式即可求得答案.
(1)由题意可得∠ADC=![]() ∠CAD
∠CAD![]() ∠ACD =
∠ACD =![]() ,∠BCA=
,∠BCA=![]() ,
,
在△ACD中,由正弦定理可得:![]() ,
,
则AC=![]() ,
,
在△ABC中,由正弦定理可得:![]() ,
,
则AB=![]()
![]()
![]() .
.
即得![]()
![]() .
.
(2)由(1)得AC=![]() ,AB=
,AB=![]() ,
,
在△ABC中,由正弦定理可得:![]() ,
,
则![]() ,
,
所以![]() .
.
由![]() 可得
可得![]() ,可得当
,可得当![]() ,即
,即![]() 时
时![]() ,
,
即当公司设置![]() 的值为
的值为![]() 时,灯柱AB和灯杆BC所用材料的总长度最小,最小值为
时,灯柱AB和灯杆BC所用材料的总长度最小,最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目