Question

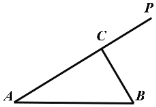
【题目】从某自动包装机包袋的食盐中,随机抽取袋作为样本,按各袋的质量（单位： ）分成四组, ,相应的样本频率分布直方图如图所示.

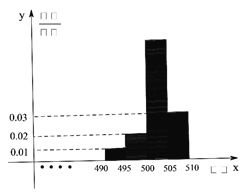
（Ⅰ）估计样本的中位数是多少？落入的频数是多少？

（Ⅱ）现从这台自动包装机包袋的大批量食盐中,随机抽取袋,记表示食盐质量属于的袋数,依样本估计总体的统计思想,求的分布列及期望.

Answer 1

【答案】（Ⅰ）见解析.（Ⅱ）见解析.

【解析】试题分析：（Ⅰ）根据频率分布直方图，即可得到样本的中位数和落入的频数；

（Ⅱ）由题意，得到随机变量的所有可能取值，计算随机变量取每个值的概率，即可得到随机变量的分布列，利用公式求解数学期望．

试题解析：

（Ⅰ）估计样本的中位数为;

落入的频数为： 袋.

（Ⅱ）随机变量的所有可能取值为

且, , ,

.

随机变量的分布列是:

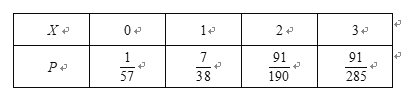
数学期望.