题目内容
【题目】 已知△ABC的三个内角A，B，C的对边分别为a，b，c，向量m＝
，n＝
，且m与n的夹角为
.
(1)求角C；
(2)已知c＝
，S△ABC＝
，求a＋b的值．
【答案】（1）
（2）
【解析】
试题（1）先根据向量数量积得夹角的关系，再根据二倍角余弦公式得cos C的值，解得角C；（2）由三角形面积公式得ab＝6，再根据余弦定理求a＋b的值．
试题解析: 解：(1)因为向量m＝
，n＝（cos
，－sin，）
所以m·n＝cos2－sin2，|m|＝
＝1，|n|＝
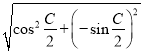＝1，
又m与n的夹角为，所以cos＝
＝cos2－sin2＝cos C＝
，
因为0<C<π，所以C＝.
(2)因为S△ABC＝absin C＝absin＝
ab，
所以ab＝
，所以ab＝6，
由余弦定理得，cos C＝
，
即＝
＝
，
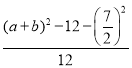解得a＋b＝.
练习册系列答案
培优三好生系列答案
相关题目
【题目】某同学参加社会实践活动，随机调查了某小区5个家庭的年可支配收入x（单位：万元）与年家庭消费y（单位：万元）的数据，制作了对照表：
x/万元 | 2.7 | 2.8 | 3.1 | 3.5 | 3.9 |
y/万元 | 1.4 | 1.5 | 1.6 | 1.8 | 2.2 |
由表中数据得回归直线方程为
，得到下列结论，其中正确的是（ ）
A.若某户年可支配收入为4万元时，则年家庭消费约为2.3万元
B.若某户年可支配收入为4万元时，则年家庭消费约为2.1万元
C.若年可支配收入每增加1万元，则年家庭消费相应平均增加0.5万元
D.若年可支配收入每增加1万元，则年家庭消费相应平均增加0.1万元
