[题目]已知函数f(x)=x2+的两个零点分别在区间内.则实数m的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数f（x）=x2+（m+2）x+（2m+5）（m≠0）的两个零点分别在区间（﹣1，0）和区间（1，2）内，则实数m的取值范围是．

【答案】﹣ ＜m＜﹣
【解析】解：由f（x）=x2+（m+2）x+（2m+5）（m≠0）的图像开口向上，两个零点分别在区间（﹣1，0）和区间（1，2）内，则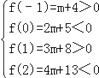解不等式可得﹣ ＜m＜﹣
所以答案是：﹣ ＜m＜﹣ ．
【考点精析】利用二次函数的性质和函数的零点与方程根的关系对题目进行判断即可得到答案，需要熟知当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；二次函数的零点：（1）△＞0，方程有两不等实根，二次函数的图象与轴有两个交点，二次函数有两个零点;（2）△＝0，方程有两相等实根（二重根），二次函数的图象与轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程无实根，二次函数的图象与轴无交点，二次函数无零点．

练习册系列答案

游戏1	游戏2	游戏3
袋中装有3个黑球和2个白球	袋中装有2个黑球和2个白球	袋中装有3个黑球和1个白球
从袋中取出2个球	从袋中取出2个球	从袋中取出2个球
若取出的两个球同色，则甲胜	若取出的两个球同色，则甲胜	若取出的两个球同色，则甲胜
若取出的两个球不同色，则乙胜	若取出的两个球不同色，则乙胜	若取出的两个球不同色，则乙胜

问其中不公平的游戏是（）
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3

【题目】定义域为R的奇函数f（x）= ，其中h（x）是指数函数，且h（2）=4．
（1）求函数f（x）的解析式；
（2）求不等式f（2x﹣1）＞f（x+1）的解集．

【题目】为了解某社区居民的家庭年收入与年支出的关系，相关部门随机调查了该社区5户家庭，得到如表统计数据表：

收入x（万元）	8.2	8.6	10.0	11.3	11.9
支出y（万元）	6.2	7.5	8.0	8.5	9.8

（1）根据上表可得回归直线方程 = x+ ，其中 =0.76， = ﹣ ，据此估计，该社区一户年收入为15万元的家庭年支出为多少？
（2）若从这5个家庭中随机抽选2个家庭进行访谈，求抽到家庭的年收入恰好一个不超过10万元，另一个超过11万元的概率．

【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车．但不知道具体谁先谁后．他打算：第一辆看后一定不坐，若第二辆比第一辆舒服，则乘第二辆；否则坐第三辆．问张先生坐到好车的概率和坐到差车的概率分别是（）
A. 、
B. 、
C. 、
D. 、

【题目】已知向量 =（sinθ，﹣2）与 =（1，cosθ）互相垂直，其中θ∈（0，）．
（Ⅰ）求sinθ和cosθ的值；
（Ⅱ）若sin（θ﹣φ）= ，0＜φ＜，求cosφ的值．

【题目】已知函数f（x）= ，g（x）=f（x）﹣a
（1）当a=2时，求函数g（x）的零点；
（2）若函数g（x）有四个零点，求a的取值范围；
（3）在（2）的条件下，记g（x）得四个零点分别为x1 ， x2 ， x3 ， x4 ，求x1+x2+x3+x4的取值范围．

【题目】已知向量 =（cos ，sin ）， =（cos ，﹣sin ），且x∈[ ，π]．
（1）求及| + |；
（2）求函数f（x）= +| + |的最大值，并求使函数取得最大值时x的值．

【题目】袋中有质地、大小完全相同的5个小球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏．甲先摸出一个球．记下编号，放回后再摸出一个球，记下编号，如果两个编号之和为偶数．则算甲赢，否则算乙赢．
（1）求甲赢且编号之和为6的事件发生的概率：
（2）试问：这种游戏规则公平吗．请说明理由．

试题分类