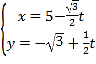题目内容
【题目】如图(1),在等腰直角![]() 中,斜边
中,斜边![]() ,D为
,D为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠得到如图(2)所示的三棱锥
折叠得到如图(2)所示的三棱锥![]() ,若三棱锥
,若三棱锥![]() 的外接球的半径为
的外接球的半径为![]() ,则
,则![]() _________.
_________.
图(1)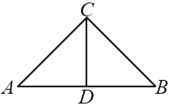 图(2)
图(2) 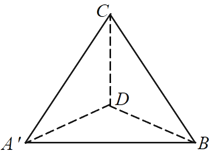
【答案】![]()
【解析】
根据题意,先找到球心的位置,再根据球的半径是![]() ,以及已有的边的长度和角度关系,分析即可解决.
,以及已有的边的长度和角度关系,分析即可解决.
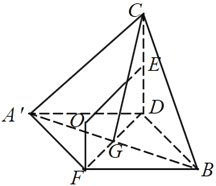
解:球是三棱锥C﹣A'BD的外接球,所以球心O到各顶点的距离相等,如图.
根据题意,CD⊥平面A'BD,
取CD的中点E,A'B的中点G,连接CG,DG,
因为A'D=BD,CD⊥平面A'BD,
所以A'和B关于平面CDG对称,
在平面CDG内,作线段CD的垂直平分线,则球心O在线段CD的垂直平分线上,设为图中的O点位置,过
O作直线CD的平行线,交平面A'BD于点F,
则OF⊥平面A'BD,且OF=DE=1,
因为A'F在平面A'BD内,所以OF⊥A'F,
即三角形A'OF为直角三角形,且斜边OA'=R![]() ,
,
∴A'F![]() 2,
2,
所以,BF=2,
所以四边形A'DBF为菱形,
又知OD=R,三角形ODE为直角三角形,
∴OE![]() 2,
2,
∴三角形A'DF为等边三角形,
∴∠A'DF![]() ,
,
故∠A'DB![]() ,
,
故填:![]() .
.

练习册系列答案
相关题目