题目内容
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
【答案】![]()
【解析】
设△BDC的中心为O1,球O的半径为R,连接oO1D,OD,O1E,OE,可得R2=3+(3﹣R)2,解得R=2,过点E作圆O的截面,当截面与OE垂直时,截面的面积最小,当截面过球心时,截面面积最大,即可求解.
如图,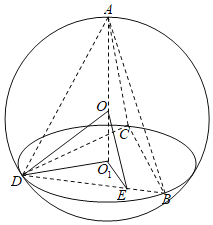
设△BDC的中心为O1,球O的半径为R,
连接oO1D,OD,O1E,OE,
则![]() ,AO1
,AO1![]()
在Rt△OO1D中,R2=3+(3﹣R)2,解得R=2,
∵BD=3BE,∴DE=2
在△DEO1中,O1E![]()
∴![]()
过点E作圆O的截面,当截面与OE垂直时,截面的面积最小,
此时截面圆的半径为![]() ,最小面积为2π.
,最小面积为2π.
当截面过球心时,截面面积最大,最大面积为4π.
故答案为:[2π,4π]

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

