题目内容
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为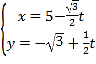 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
【答案】(1)直线l的直角坐标方程为![]() ;圆C的直角坐标方程为
;圆C的直角坐标方程为![]() ;
;
(2)![]() ;
;
【解析】
(1)由直线l的参数方程,消去参数t,即可得到直线l的直角坐标方程,再由极坐标与直角坐标的互化公式,即可求得圆C的直角坐标方程;
(2)设![]() ,化简得
,化简得![]() ,结合三角函数的性质,即可求解.
,结合三角函数的性质,即可求解.
(1)由题意,直线l的参数方程为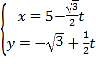 (t为参数),
(t为参数),
消去参数t,得直线l的直角坐标方程为![]() ,
,
又由圆C的极坐标方程为![]() ,即
,即![]() ,
,
又因为![]() ,
,![]() ,
,![]() ,
,
可得圆C的直角坐标方程为![]() .
.
(2)因为点![]() 在圆C上,可设
在圆C上,可设![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | |
男生 | 5 | |
女生 | 10 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由;
(3)在上述喜好体育运动的6人中随机抽取两人,求恰好抽到一男一女的概率.
参考公式:![]() .
.
独立性检验临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |