题目内容
(本小题满分14分)
已知函数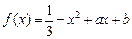 的图像在点P(0,f(0))处的切线方程为
的图像在点P(0,f(0))处的切线方程为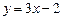 .
.
(Ⅰ)求实数a,b的值;
(Ⅱ)设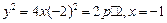
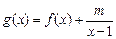 是
是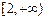 上的增函数.
上的增函数.
(ⅰ)求实数m的最大值;
(ⅱ)当m取最大值时,是否存在点Q,使得过点Q的直线能与曲线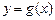 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
已知函数
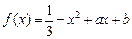 的图像在点P(0,f(0))处的切线方程为
的图像在点P(0,f(0))处的切线方程为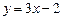 .
.(Ⅰ)求实数a,b的值;
(Ⅱ)设
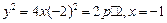
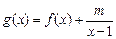 是
是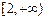 上的增函数.
上的增函数.(ⅰ)求实数m的最大值;
(ⅱ)当m取最大值时,是否存在点Q,使得过点Q的直线能与曲线
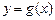 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.(I)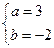 (II)(ⅰ)
(II)(ⅰ)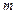 的最大值为3(ⅱ)存在点
的最大值为3(ⅱ)存在点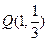 ,使得过点
,使得过点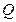 的直线若能与函数
的直线若能与函数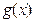 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
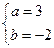 (II)(ⅰ)
(II)(ⅰ)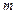 的最大值为3(ⅱ)存在点
的最大值为3(ⅱ)存在点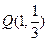 ,使得过点
,使得过点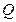 的直线若能与函数
的直线若能与函数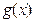 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。本小题主要考察函数、导数等基础知识,考察推力论证能力、抽象概况能力、运算求解能力,考察函数与方程思想、数形结合思想、化归与转换思想、分类与整合思想。满分14分。
解法一:
(Ⅰ)由 及题设得
及题设得 即
即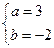 。
。
(Ⅱ)(ⅰ)由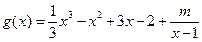
得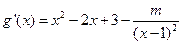 。
。
 是
是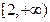 上的增函数,
上的增函数,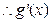
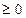 在
在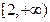 上恒成立,
上恒成立,
即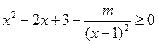 在
在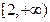 上恒成立。
上恒成立。
设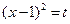 。
。
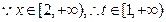 ,
,
即不等式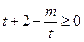 在
在 上恒成立
上恒成立
当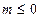 时,不等式
时,不等式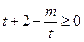 在
在 上恒成立。
上恒成立。
当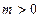 时,设
时,设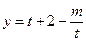 ,
,
因为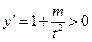 ,所以函数
,所以函数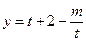 在
在 上单调递增,
上单调递增,
因此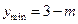 。
。
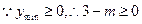 ,即
,即 。
。
又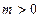 ,故
,故 。
。
综上,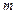 的最大值为3。
的最大值为3。
(ⅱ)由(ⅰ)得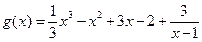 ,其图像关于点
,其图像关于点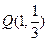 成中心对称。
成中心对称。
证明如下:

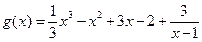
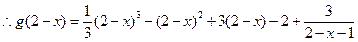
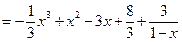
因此, 。
。
上式表明,若点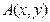 为函数
为函数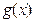 在图像上的任意一点,则点
在图像上的任意一点,则点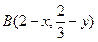 也一定在函数
也一定在函数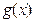 的图像上。而线段
的图像上。而线段 中点恒为点
中点恒为点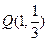 ,由此即知函数
,由此即知函数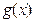 的图像关于点
的图像关于点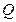 成中心对称。
成中心对称。
这也就表明,存在点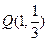 ,使得过点
,使得过点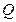 的直线若能与函数
的直线若能与函数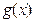 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
解法二:
(Ⅰ)同解法一。
(Ⅱ)(ⅰ)由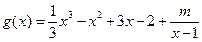
得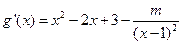 。
。
 是
是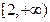 上的增函数,
上的增函数,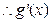
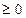 在
在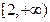 上恒成立,
上恒成立,
即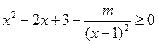 在
在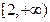 上恒成立。
上恒成立。
设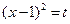 。
。
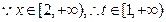 ,
,
即不等式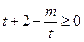 在
在 上恒成立。
上恒成立。
所以 在
在 上恒成立。
上恒成立。
令 ,
, ,可得
,可得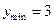 ,故
,故 ,即
,即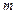 的最大值为
的最大值为 3.
3.
(ⅱ)由(ⅰ)得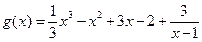 ,
,
将函数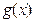 的图像向左平移1个长度单位,再向下平移
的图像向左平移1个长度单位,再向下平移 个长度单位,所得图像相应的函数解析式为
个长度单位,所得图像相应的函数解析式为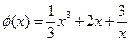 ,
, 。
。
由于 ,所以
,所以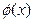 为奇函数,故
为奇函数,故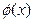 的图像关于坐标原点成中心对称。
的图像关于坐标原点成中心对称。
由此即得,函数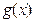 的图像关于点
的图像关于点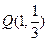 成中心对称。
成中心对称。
这也表明,存在点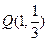 ,是得过点
,是得过点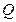 的直线若能与函数
的直线若能与函数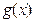 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
解法一:
(Ⅰ)由
 及题设得
及题设得 即
即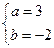 。
。(Ⅱ)(ⅰ)由
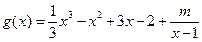
得
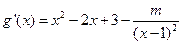 。
。 是
是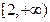 上的增函数,
上的增函数,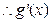
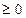 在
在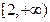 上恒成立,
上恒成立,即
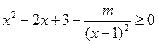 在
在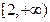 上恒成立。
上恒成立。设
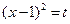 。
。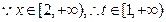 ,
,即不等式
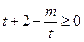 在
在 上恒成立
上恒成立当
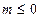 时,不等式
时,不等式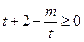 在
在 上恒成立。
上恒成立。当
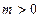 时,设
时,设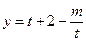 ,
,
因为
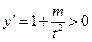 ,所以函数
,所以函数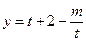 在
在 上单调递增,
上单调递增,因此
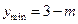 。
。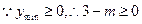 ,即
,即 。
。又
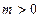 ,故
,故 。
。综上,
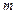 的最大值为3。
的最大值为3。(ⅱ)由(ⅰ)得
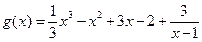 ,其图像关于点
,其图像关于点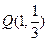 成中心对称。
成中心对称。证明如下:

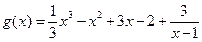
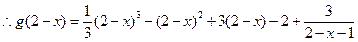
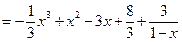
因此,
 。
。上式表明,若点
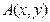 为函数
为函数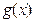 在图像上的任意一点,则点
在图像上的任意一点,则点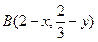 也一定在函数
也一定在函数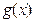 的图像上。而线段
的图像上。而线段 中点恒为点
中点恒为点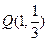 ,由此即知函数
,由此即知函数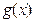 的图像关于点
的图像关于点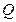 成中心对称。
成中心对称。这也就表明,存在点
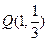 ,使得过点
,使得过点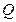 的直线若能与函数
的直线若能与函数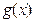 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。解法二:
(Ⅰ)同解法一。
(Ⅱ)(ⅰ)由
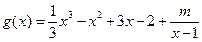
得
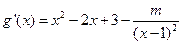 。
。 是
是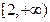 上的增函数,
上的增函数,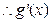
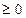 在
在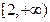 上恒成立,
上恒成立,即
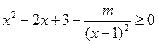 在
在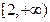 上恒成立。
上恒成立。设
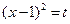 。
。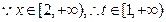 ,
,即不等式
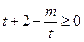 在
在 上恒成立。
上恒成立。所以
 在
在 上恒成立。
上恒成立。令
 ,
, ,可得
,可得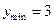 ,故
,故 ,即
,即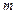 的最大值为
的最大值为 3.
3.(ⅱ)由(ⅰ)得
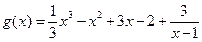 ,
,将函数
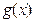 的图像向左平移1个长度单位,再向下平移
的图像向左平移1个长度单位,再向下平移 个长度单位,所得图像相应的函数解析式为
个长度单位,所得图像相应的函数解析式为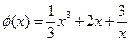 ,
, 。
。由于
 ,所以
,所以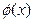 为奇函数,故
为奇函数,故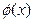 的图像关于坐标原点成中心对称。
的图像关于坐标原点成中心对称。
由此即得,函数
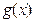 的图像关于点
的图像关于点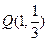 成中心对称。
成中心对称。这也表明,存在点
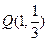 ,是得过点
,是得过点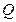 的直线若能与函数
的直线若能与函数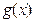 的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
的图像围成两个封闭图形,则这两个封闭图形的面积总相等。
练习册系列答案
相关题目
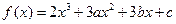 在
在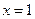 及
及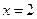 时取得极值.
时取得极值.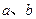 的值;
的值;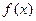 在
在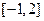 上的最大值是9,求
上的最大值是9,求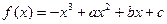 图象上的点
图象上的点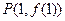 处的切线方程为
处的切线方程为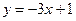 。若函数
。若函数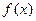 在
在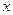 =-2处有极值,求
=-2处有极值,求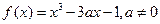 .
.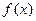 的单调区间;
的单调区间; 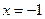 处取得极值,直线
处取得极值,直线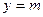 与
与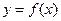 的图象有三个不同的交点,求
的图象有三个不同的交点,求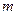 的取值范围。
的取值范围。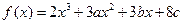 在
在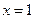 及
及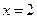 时取得极值.
时取得极值.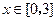 ,都有
,都有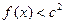 成立,求c的取值范围.
成立,求c的取值范围.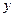 =
= 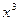 -12
-12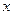 +16在 [-3,3]上的最大值、最小值分别是( )
+16在 [-3,3]上的最大值、最小值分别是( )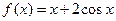 在
在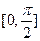 取最大值时,
取最大值时,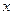 的值为_________
的值为_________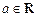 ,若函数
,若函数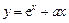 ,
,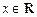 ,有大于零的极值点,则
,有大于零的极值点,则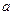 的取值范
的取值范 围是 .
围是 .