题目内容
已知圆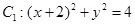 及点
及点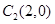 ,在圆
,在圆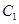 上任取一点
上任取一点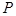 ,连接
,连接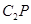 ,做线段
,做线段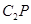 的中垂线交直线
的中垂线交直线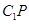 于点
于点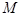 .
.
(1)当点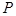 在圆
在圆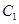 上运动时,求点
上运动时,求点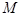 的轨迹
的轨迹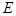 的方程;
的方程;
(2)设轨迹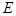 与
与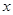 轴交于
轴交于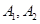 两点,在轨迹
两点,在轨迹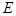 上任取一点
上任取一点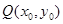
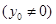 ,直线
,直线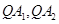 分别交
分别交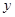 轴于
轴于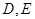 两点,求证:以线段
两点,求证:以线段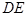 为直径的圆
为直径的圆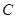 过两个定点,并求出定点坐标.
过两个定点,并求出定点坐标.
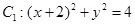 及点
及点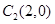 ,在圆
,在圆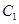 上任取一点
上任取一点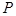 ,连接
,连接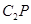 ,做线段
,做线段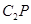 的中垂线交直线
的中垂线交直线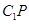 于点
于点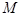 .
.(1)当点
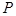 在圆
在圆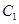 上运动时,求点
上运动时,求点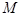 的轨迹
的轨迹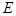 的方程;
的方程;(2)设轨迹
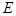 与
与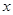 轴交于
轴交于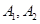 两点,在轨迹
两点,在轨迹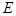 上任取一点
上任取一点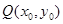
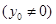 ,直线
,直线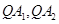 分别交
分别交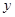 轴于
轴于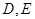 两点,求证:以线段
两点,求证:以线段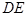 为直径的圆
为直径的圆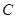 过两个定点,并求出定点坐标.
过两个定点,并求出定点坐标.(1) 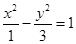
(2)证明见解析,定点为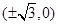
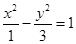
(2)证明见解析,定点为
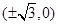
本试题主要考查了运用双曲线定义求解轨迹方程,以及利用直径的两端点坐标求解圆的方程的综合运用试题。
解:(1)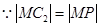 ,
,
又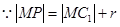
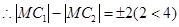
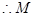 点轨迹是以
点轨迹是以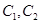 为焦点的双曲线
为焦点的双曲线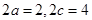
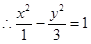 ……………4分
……………4分
(2)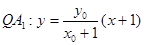
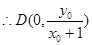
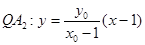
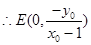
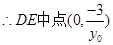 ……………8分
……………8分
以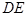 为直径的圆方程
为直径的圆方程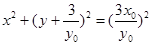 ……………9分
……………9分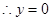 时,
时,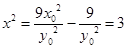 ……………11分
……………11分
定点为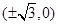
解:(1)
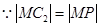 ,
,又
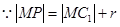
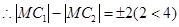
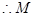 点轨迹是以
点轨迹是以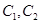 为焦点的双曲线
为焦点的双曲线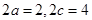
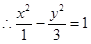 ……………4分
……………4分(2)
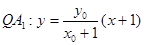
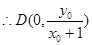
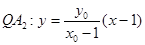
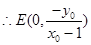
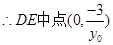 ……………8分
……………8分以
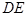 为直径的圆方程
为直径的圆方程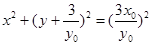 ……………9分
……………9分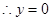 时,
时,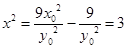 ……………11分
……………11分定点为
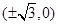

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
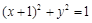 及圆
及圆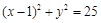 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .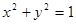 和
和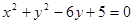 的位置关系为( )
的位置关系为( )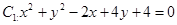 和圆
和圆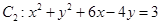 的位置关系是
的位置关系是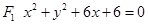 相外切,与圆
相外切,与圆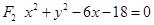 相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。
相内切求动圆圆心的轨迹曲线E的方程,并说明它是什么曲线。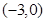 作一直线
作一直线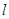 与曲线E交与A,B两点,若
与曲线E交与A,B两点,若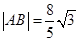 ,求此时直线
,求此时直线 与
与 外切,则
外切,则 的最大值为
的最大值为 



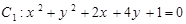 与圆
与圆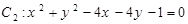 的公切线有几条( )
的公切线有几条( )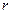 >0,两圆
>0,两圆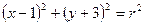 与
与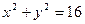 可能( )
可能( )