题目内容
已知动圆C与圆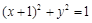 及圆
及圆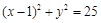 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .
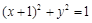 及圆
及圆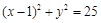 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .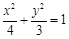 .
.试题分析:记两已知圆圆心为A(-1,0),B(1,0),设动圆半径为r,由动圆和两已知圆都内切得:
BC+r=5,AC+1=r,两式相加得BC+AC=4>AB=2,所以C的轨迹是椭圆,即可得其轨迹方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
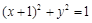 及圆
及圆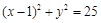 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .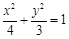 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案