题目内容
((本小题满分12分)
数列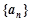 各项均为正数,其前
各项均为正数,其前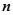 项和为
项和为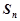 ,且满足
,且满足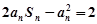 .
.
(Ⅰ)求证数列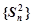 为等差数列,并求数列
为等差数列,并求数列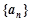 的通项公式;
的通项公式;
(Ⅱ)设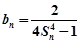 , 求数列
, 求数列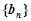 的前n项和
的前n项和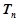 ,并求使
,并求使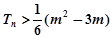 对所
对所
有的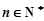 都成立的最大正整数m的值.
都成立的最大正整数m的值.
数列
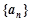 各项均为正数,其前
各项均为正数,其前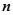 项和为
项和为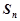 ,且满足
,且满足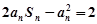 .
.(Ⅰ)求证数列
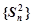 为等差数列,并求数列
为等差数列,并求数列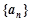 的通项公式;
的通项公式;(Ⅱ)设
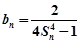 , 求数列
, 求数列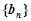 的前n项和
的前n项和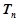 ,并求使
,并求使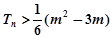 对所
对所有的
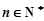 都成立的最大正整数m的值.
都成立的最大正整数m的值.解:(Ⅰ)∵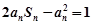 ,∴当n≥2时,
,∴当n≥2时,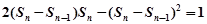 ,
,
整理得,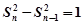 (n≥2),(2分)又
(n≥2),(2分)又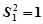 , (3分)
, (3分)
∴数列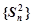 为首项和公差都是1的等差数列. (4分)
为首项和公差都是1的等差数列. (4分)
∴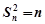 ,又
,又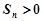 ,∴
,∴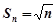 (5分)
(5分)
∴n≥2时,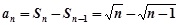 ,又
,又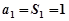 适合此式 (6分)
适合此式 (6分)
∴数列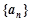 的通项公式为
的通项公式为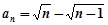 (7分)
(7分)
(Ⅱ)∵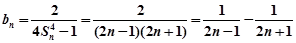 (8分)
(8分)
∴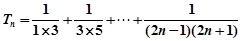
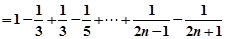 =
=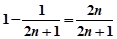 (10分)
(10分)
∴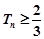 ,依题意有
,依题意有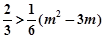 ,解得
,解得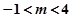 ,
,
故所求最大正整数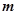 的值为3 (12分)
的值为3 (12分)
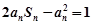 ,∴当n≥2时,
,∴当n≥2时,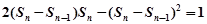 ,
, 整理得,
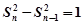 (n≥2),(2分)又
(n≥2),(2分)又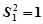 , (3分)
, (3分)∴数列
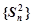 为首项和公差都是1的等差数列. (4分)
为首项和公差都是1的等差数列. (4分)∴
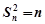 ,又
,又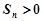 ,∴
,∴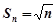 (5分)
(5分)∴n≥2时,
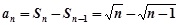 ,又
,又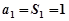 适合此式 (6分)
适合此式 (6分)∴数列
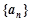 的通项公式为
的通项公式为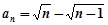 (7分)
(7分)(Ⅱ)∵
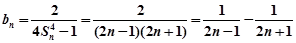 (8分)
(8分)∴
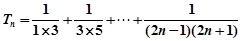
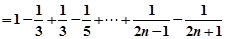 =
=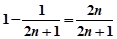 (10分)
(10分)∴
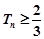 ,依题意有
,依题意有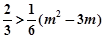 ,解得
,解得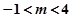 ,
,故所求最大正整数
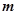 的值为3 (12分)
的值为3 (12分)略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
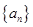 满足
满足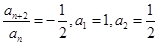 ,则
,则 。
。 的定义域为R,数列
的定义域为R,数列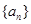 满足
满足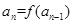 (
(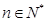 且
且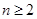 ).
).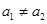 ,且
,且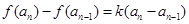 (k为非零常数,
(k为非零常数, 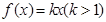 ,
,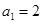 ,
,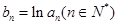 ,数列
,数列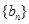 的前n项和为
的前n项和为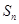 ,对于给定的正整数
,对于给定的正整数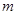 ,如果
,如果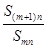 的值与n无关,求k的值.
的值与n无关,求k的值.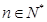 时,
时,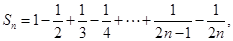
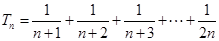 .
.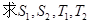 ;(II)
;(II)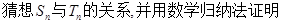 .
.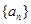 的公差
的公差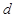 大于0,且
大于0,且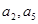 是方程
是方程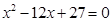 的两根,数列
的两根,数列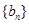 的前
的前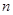 项和为
项和为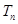 ,且
,且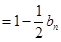
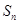 ,试比较
,试比较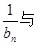
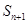 的大小,并说明理由.
的大小,并说明理由.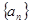 的前
的前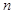 项和为
项和为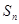 ,点
,点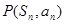 在直线
在直线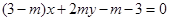 上,(
上,(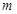 为常数,
为常数,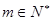 ,
,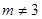 ).
).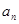 ;
;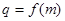 ,数列
,数列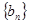 满足
满足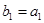 ,
,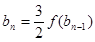 ,
,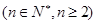 ,求证:
,求证: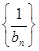 为等差
为等差 数列,并求
数列,并求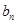 ;
;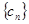 满足
满足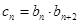 ,
,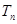 为数列
为数列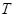 满足
满足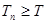
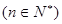 ,求
,求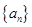 满足
满足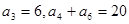 。
。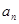 ;
;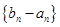 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列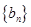 的通项公式及其前
的通项公式及其前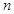 项和
项和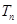 .
.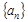 的前n 项和Sn满足:Sn= 2an+1.
的前n 项和Sn满足:Sn= 2an+1.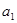 ,
,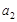 ,
,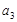 ;
;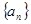 中,
中,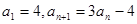 ,则数列
,则数列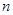 项和
项和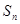 = .
= .