Question

【题目】已知 、 是两个不共线的向量，且 =（cosα，sinα）， =（cosβ，sinβ）．
（1）求证： + 与 ﹣ 垂直；
（2）若α∈（﹣ ， ），β= ，且| + |= ，求sinα．

Answer 1

【答案】
（1）证明： 、 是两个不共线的向量，

且 =（cosα，sinα）， =（cosβ，sinβ），．

∴ + =（cosα+cosβ，sinα+sinβ），

﹣ =（cosα﹣cosβ，sinα﹣sinβ），

∴（ + ）（ ﹣ ）=（cos2﹣cos2β）+（sin2α﹣sin2β）

=（cos2α+sin2α）﹣（cos2β+sin2β）

=1﹣1=0，

∴ + 与 ﹣ 垂直

（2）解：∵ =（cosα+cosβ）2+（sinα+sinβ）2

=2+2（cosαcosβ+sinαsinβ）

=2+2cos（α﹣β），

且β= ，| + |= ，

∴2+2cos（α﹣ ）= ，

解得cos（α﹣ ）= ；

又α∈（﹣ ， ），

∴α﹣ ∈（﹣ ，0），

∴sin（α﹣ ）=﹣ =﹣ ，

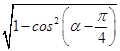∴sinα=sin[（α﹣ ）+ ]=sin（α﹣ ）cos +cos（α﹣ ）sin

=﹣ × + × =﹣

【解析】（1）利用平面向量的坐标运算与数量积为0，即可证明 + 与 ﹣ 垂直；（2）利用平面向量的数量积与模长公式，结合三角恒等变换与同角的三角函数关系，即可求出sinα的值．