题目内容
【题目】圆C满足：①圆心C在射线y=2x（x＞0）上； ②与x轴相切；
③被直线y=x+2截得的线段长为 
（1）求圆C的方程；
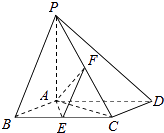
（2）过直线x+y+3=0上一点P作圆C的切线，设切点为E、F，求四边形PECF面积的最小值，并求此时 
的值．
【答案】
（1）解：圆心C的坐标为（a，2a）（a＞0），半径为r．
则有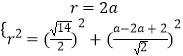 
，解得 
∴圆C的方程为（x﹣1）2+（y﹣2）2=4
（2）解：由切线的性质知：四边形PECF的面积S=|PE|r=r 
= 
∴四边形PECF的面积取最小值时，|PC|最小，
即为圆心C（1，2）到直线x+y+3=0的距离d=3 
．
∴|PC|最小为 
∴四边形PEMF的面积S的最小值为2 
此时| 
|=| 
|= ，设∠CPE=∠CPF=α，则 
∴ 
=| |2cos2α=| |2 （1﹣2sin2α）= 
【解析】（1）圆心C的坐标为（a，2a）（a＞0），半径为r，利用条件建立方程组，即可求圆C的方程；（2）四边形PECF的面积取最小值时，|PC|最小，从而可求 的值．
练习册系列答案
相关题目
