Question

【题目】已知函数 sin（π﹣2x）
（1）若 ，求f（x）的取值范围；
（2）求函数 f（x）的单调增区间．

Answer 1

【答案】
（1）解：函数 sin（π﹣2x）

=2cos2x+ sin2x

=cos2x+ sin2x+1

=2sin（2x+ ）+1，

当 时， ，

故 ，

，

所以f（x）的取值范围是[0，3]

（2）解：由题意有 ，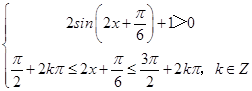

解得 ，

即 +2kπ≤2x+ ＜ +2kπ，k∈Z，

所以 +kπ≤x＜ +kπ，k∈Z；

所以函数 的单调增区间为[ +kπ， +kπ），k∈Z．

【解析】（1）化函数f（x）为正弦型函数，求出 时f（x）的取值范围即可；（2）根据复合函数的单调性列出不等式组，求出x的取值范围即可．
【考点精析】通过灵活运用复合函数单调性的判断方法和三角函数的最值，掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”；函数，当时，取得最小值为；当时，取得最大值为，则，，即可以解答此题．