题目内容
【题目】正三角形
的边长为2，将它沿高
翻折，使点
与点
间的距离为
，此时四面体
外接球表面积为__________．
【答案】
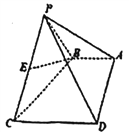
【解析】分析：由题意将几何体补形为三棱柱，结合三棱柱的几何特征整理计算即可求得最终结果.
详解：根据题意可知三棱锥BACD的三条侧棱BD⊥AD、DC⊥DA，
底面是等腰三角形，它的外接球就是它扩展为三棱柱的外接球，
求出三棱柱的底面中心连线的中点到顶点的距离，就是球的半径，
三棱柱的底面边长为1,1,
，
由题意可得：三棱柱上下底面中点连线的中点，到三棱柱顶点的距离相等，说明中心就是外接球的球心，
∴三棱柱的外接球的球心为O，外接球的半径为r，
棱柱的高为,球心到底面的距离为
，
三棱柱中,底面△BDC,BD=CD=1,BC=,∴∠BDC=120°，
△BDC的外接圆的半径为：
，
∴球的半径为
.
外接球的表面积为：
.
故答案为：.
练习册系列答案
相关题目
