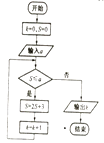
题目内容
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.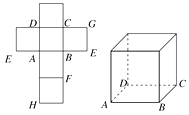
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
【答案】
(1)解:点F、G、H的位置如图所示.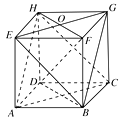
(2)解:平面BEC∥平面ACH . 证明如下:
因为ABCD-EFGH为正方体,所以BC∥FG , BC=FG ,
又FG∥EH , FG=EH , 所以BC∥EH , BC=EH ,
于是四边形BCEH为平行四边形,
所以BE∥CH ,
又CH平面ACH , BE平面ACH ,
所以BE∥平面ACH ,
同理,BG∥平面ACH ,
又BE∩BG=B ,
所以平面BEG∥平面ACH .
(3)证明:连接FH交EG于点O , 连接BD .
因为ABCD-EFGH为正方体,所以DH⊥平面EFGH ,
因为EG平面EFGH , 所以DH⊥EG ,
又EG⊥FH , EG∩FH=O ,
所以EG⊥平面BFHD ,
又DF平面BFHD , 所以DF⊥EG ,
同理DF⊥BG ,
又EG∩BG=G ,
所以DF⊥平面BEG .
【解析】(1)将该正方体的展开还原为空间几何体即可。
(2)重点考查了平面与平面平行的判定:一个平面内的两条相交直线平行于另一个平面,则这两平面平行.
(3)重点考查了直线与平面垂直的判定:若一条直线垂直于一个平面内两条相交直线,则该直线与此平面垂直。

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的 ![]() 列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(参考公式 ![]() ,其中
,其中 ![]() .)
.)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |

(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)