题目内容
【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,上顶点为
,上顶点为 ![]() ,
, ![]() 周长为
周长为 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)若点 ![]() 是椭圆
是椭圆 ![]() 上第一象限内的一个点,直线
上第一象限内的一个点,直线 ![]() 过点
过点 ![]() 且与直线
且与直线 ![]() 平行,直线
平行,直线 ![]() 且
且 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于点
交于点 ![]() ,是否存在常数
,是否存在常数 ![]() ,使
,使 ![]() .若存在,求出
.若存在,求出 ![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】
(1)解:由题意知 ![]() ,
, ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
∴椭圆 ![]() 的方程为
的方程为 ![]() .
.
(2)解:由 ![]() 得
得 ![]() ,∴
,∴ ![]() ,
,
又 ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() 的方程为
的方程为 ![]() ,可设
,可设 ![]() 方程为
方程为 ![]() ,
,
由 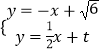 得
得 ![]() ,
,
由 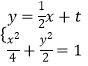 得
得 ![]() ,
, ![]() ,
, ![]() ,
,
设 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
,
由弦长公式: ![]() ,
,
同理, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴存在常数 ![]() ,使
,使 ![]()
【解析】(1)考查了椭圆的几何性质与标准方程。
(2)考查了椭圆的综合应用、弦长公式。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目