题目内容
11.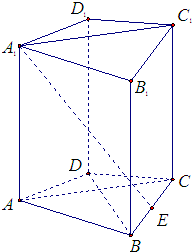 如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,
如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求证:A1E∥平面DCC1D1
(Ⅲ) 若AA1⊥AC,求A1E与面ACC1A1所成角大小.
分析 (Ⅰ)利用垂直平分线的判定定理即可得到BD垂直平分AC,利用面面垂直的性质定理即可得到BD⊥平面AA1C1C,利用线面垂直的性质定理即可证明结论;
(Ⅱ)利用△OCD的边角关系即可得到∠OCD=30°,从而得到∠BCD=90°,DC⊥BC,利用等边三角形的性质即可得到AE⊥BC,得到AE∥DC,再利用线面平行的判定定理即可证明结论;
(Ⅲ)过E作AC的垂线,设垂足为N,利用面ABCD⊥面AA1C1C,可得EN⊥面AA1C1C,连A1N,则A1N为A1E在面AA1C1C内的射影,∠EA1N为直线A1E与面AC1所成角,即可求A1E与面ACC1A1所成角大小.
解答  (Ⅰ)证明:在四棱锥ABCD-A1B1C1D1中,
(Ⅰ)证明:在四棱锥ABCD-A1B1C1D1中,
∵AB=BC=CA,且AD=DC,
取AC中点O,则BO⊥AC,DO⊥AC,∴B,O,D三点在一条直线上.
又∵面AA1C1C⊥面ABCD,面AA1C1C∩面ABCD=AC,BD?面ABCD,BD⊥AC,
∴BD⊥面AA1C1C,AA1?面AA1C1C,∴BD⊥AA1;…4分
(Ⅱ)证明:连AE,在Rt△DCO中∠DCO=30°
在正△BCA中,∠BCO=60°,∴DC⊥BC,
又在正△BCA中,AE⊥BC,
∴AE∥DC,
又AE?面DCC1D1,DC?面DCC1D1,∴AE∥面DCC1D1,
在四棱锥中,AA1∥DD1,AA1?面DCC1D1,DD1?面DCC1D1,
∴AA1∥面DCC1D1,
又AA1∩AE=A,
∴面A1AE∥面DCC1D1,
又A1E?面AA1E,故A1E∥面DCC1D1.
(Ⅲ)解:过E作AC的垂线,设垂足为N,∵面ABCD⊥面AA1C1C,∴EN⊥面AA1C1C,
连A1N,则A1N为A1E在面AA1C1C内的射影,
∴∠EA1N为直线A1E与面AC1所成角,
由已知得:$EN=\frac{3}{4},{A_1}N=\sqrt{A{A_1}^2+A{N^2}}=\frac{{\sqrt{43}}}{4}$,∴$tan∠E{A_1}N=\frac{{\frac{3}{4}}}{{\frac{{\sqrt{43}}}{4}}}=\frac{{3\sqrt{43}}}{43}$.
点评 熟练掌握面面垂直的性质定理、线面垂直的性质定理、线面平行的判定定理是解题的关键.

| A. | log22015 | B. | 2015 | C. | -2015 | D. | 1008 |
| A. | $({\frac{7π}{12},0})$ | B. | $({\frac{π}{3},0})$ | C. | $({\frac{11π}{6},0})$ | D. | $({\frac{3π}{2},0})$ |