题目内容

20．已知数列{an}，{bn}满足bn=log2an，n∈N*，其中{bn}是等差数列，且a8•a2008=$\frac{1}{4}$，则b1+b2+b3+…+b2015=（　　）
A．log22015B．2015C．-2015D．1008

分析 由于数列{an}，{bn}满足bn=log2an，n∈N*，其中{bn}是等差数列，可得数列{an}是等比数列，由等比数列的性质可得a1•a2015=a2•a2014=…=a1007•a1009=a10082=$\frac{1}{4}$，再利用对数的运算性质即可得出．

解答 解：∵数列{an}，{bn}满足bn=log2an，n∈N*，其中{bn}是等差数列，
∴数列{an}是等比数列，
由a8•a2008=$\frac{1}{4}$，可得a10082=$\frac{1}{4}$，即a1008=$\frac{1}{2}$，
∴a1•a2015=a2•a2014=…=a1007•a1009=a10082=$\frac{1}{4}$，
∴b1+b2+b3+…+b2015=log2（a1•a2•…•a2015）=log2（$\frac{1}{2}$）2015=-2015．
故选：C．

点评 本题考查了等差数列与等比数列的通项公式及其性质、对数的运算法则，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，离心率e=$\frac{1}{2}$，点F2到直线y=x的距离为$\frac{\sqrt{2}}{2}$
（Ⅰ）求椭圆C的方程
（Ⅱ）过F2任意作一条直线l交椭圆C于A、B两点，是否存在以线段AB为直径的圆经过F1，若存在，求出直线l方程；若不存在，请说明理由．
11．如图，在四棱柱ABCD-A1B1C1D1中，AB=BC=CA=$\sqrt{3}$，AD=CD=AA1=1，平面AA1C1C⊥平面ABCD，E为线段BC的中点，
（Ⅰ）求证：BD⊥AA1；
（Ⅱ）求证：A1E∥平面DCC1D1
（Ⅲ） 若AA1⊥AC，求A1E与面ACC1A1所成角大小．
8．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打时间x（单位：小时）与当于投篮命中率y之间的关系：
时间x12345
命中率y0.40.50.60.60.4
（Ⅰ）根据上表的数据，求出y关于x的线性回归方程y=$\widehat{b}$x+a；
（Ⅱ）预测小李该月6号打6小时篮球的投篮命中率为多少？（考点：线性回归应用）
15．由若干个棱长为1的正方体组成的几何体的三视图如图所示，则该几何体的体积为5．
5．设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x+2）=-f（x），当x∈[0，2]时，f（x）=2x-x2．
（1）当x∈[2，4]时，求f（x）的解析式；
（2）计算：f（0）+f（1）+f（2）+…+f（201）．
12．如表是对与喜欢足球与否的统计列联表依据表中的数据，得到（　　）
喜欢足球不喜欢足球总计
男402868
女51217
总计454085
A．K2=9.564B．K2=3.564C．K2＜2.706D．K2＞3.841
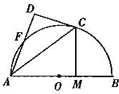9．如图，AB是圆O的直径，C、F为圆O上点，CA是∠BAF的角平分线，CD与圆O切于点C且交AF的延长线于点D，CM⊥AB，垂足为点M，求证：
（1）CD⊥AD；
（2）若圆O的半径为1，∠BAC=30°，试求DF•AM的值．
2．过抛物线C：y2=2px（p＞0）的焦点F作直线交抛物线于A、B两点，O为坐标原点，|AB|=8p，且S△AOB=4，则p的值为（　　）
A．1B．2C．4D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网