题目内容
5.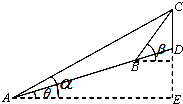 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.(1)求BC的长;
(2)若l=24,α=45°,β=75°,θ=30°,求信号塔CD的高度.
分析 (1)直接利用正弦定理列出关系式即可.
(2)通过关系式,利用正弦定理化简求解即可.
解答 (本小题满分12分)
解:(1)在△ABC中,∠CAB=α-θ,∠ABC=π-(β-θ),∠ACB=β-α,
由正弦定理,$BC=\frac{sin(α-θ)}{sin(β-α)}l$.(6分)
(2)由(1)及条件知,$BC=\frac{sin(α-θ)}{sin(β-α)}l=12(\sqrt{6}-\sqrt{2})$,∠BCD=90°-β=15°,∠CBD=β-θ=45°,∠BDC=120°,由正弦定理得,$CD=\frac{sin45°}{sin120°}•BC=24-8\sqrt{3}$.
(12分)
点评 本小题主要考查利用解三角形的思想解决实际问题,对考生的抽象概括能力和运算求解能力,化归与转化能力提出一定要求.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
13.已知集合A={x|x>-1},A∪B=A,则集合B可以是( )
| A. | {0,2} | B. | {-1,0,1} | C. | {x|x≤0} | D. | R |
10.复数z1,z2满足|z1|=|z2|=1,|z1+z2|=$\sqrt{3}$,则|z1-z2|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
15.下列函数中,既是偶函数又存在零点的是( )
| A. | y=cosx | B. | y=sinx | C. | y=lnx | D. | y=x2+1 |
 如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是
如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是