题目内容
2．以原点为顶点，以x轴正半轴为始边的角α的终边与直线y=2x-1垂直，则tan（α-$\frac{3}{4}$π）=$\frac{1}{3}$，cosα=$\frac{{2\sqrt{5}}}{5}$或$-\frac{{2\sqrt{5}}}{5}$．分析 直接利用角α的终边与直线y=2x-1垂直，求出终边所在直线的斜率，然后求出cosα，由两角差的正切函数公式即可求tan（α-$\frac{3}{4}$π）的值．
解答 解：因为角α的终边与直线y=2x-1垂直，所以终边所在的直线的斜率为：-$\frac{1}{2}$，
即tanα=-$\frac{1}{2}$，又sin2α+cos2α=1，所以cosα=$\frac{2\sqrt{5}}{5}$或-$\frac{2\sqrt{5}}{5}$，
所以：tan（α-$\frac{3}{4}$π）=$\frac{tanα-tan\frac{3π}{4}}{1+tanαtan\frac{3π}{4}}$=$\frac{（-\frac{1}{2}）-（-1）}{1+（-\frac{1}{2}）×（-1）}$=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$，$\frac{2\sqrt{5}}{5}$或-$\frac{2\sqrt{5}}{5}$．
点评 本题考查直线方程的垂直关系的应用，三角函数的定义的应用，考查计算能力．
练习册系列答案
相关题目
5．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，已知函数f（x）=$|\begin{array}{l}{π}&{x+1}\\{x-1}&{x}\end{array}|$，且△ABC是锐角三角形，则下列不等式成立的是（ ）
| A． | f（sinA）＞f（sinB） | B． | f（cosA）＞f（cosB） | C． | f（sinA）＞f（cosB） | D． | f（cosA）＞f（sinB） |
13．已知集合A={x|x＞-1}，A∪B=A，则集合B可以是（ ）
| A． | {0，2} | B． | {-1，0，1} | C． | {x|x≤0} | D． | R |
10．复数z1，z2满足|z1|=|z2|=1，|z1+z2|=$\sqrt{3}$，则|z1-z2|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
如图，已知四边形ABCD满足AD∥BC，BA=AD=DC=$\frac{1}{2}$BC=a，E是
7．
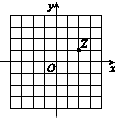若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，则复数$\frac{z}{1-2i}$的共轭复数是（ ）
若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，则复数$\frac{z}{1-2i}$的共轭复数是（ ）| A． | -$\frac{3}{5}$i | B． | -i | C． | $\frac{3}{5}$i | D． | i |