题目内容
19.定义函数g(x)={2sin7π2,x>02tan25π4,x<0,设f(x)=[g(2-x)•f1(x)]•[g(x-3)•f2(x)],x∈[0,2],其中f1(x)=x+m,f2(x)=1-x,若f(x)-20≤g(x)恒成立,则实数m的取值范围为[-92,52].分析 化简g(x),由x的范围,得到2-x,x-3的范围,化简f(x),再令h(x)=4x2+4(m-1)x-4m-20,若f(x)-20≤g(x)恒成立,则h(x)max≤-2在[0,2]恒成立.讨论二函数的对称轴和区间的关系,运用单调性得到最大值,解不等式即可得到所求范围.
解答 解:g(x)={−2,x>02,x<0,由x∈[0,2],
则-2≤-x≤0,0≤2-x≤2≤g(2-x)=-2,
同理-3≤x-3≤-1,g(x-3)=2,
则f(x)=[g(2-x)•f1(x)]•[g(x-3)•f2(x)]
=(-2)(x+m)•2(1-x)=4(x-1)(x+m)=4x2+4(m-1)x-4m,
令h(x)=4x2+4(m-1)x-4m-20,
若f(x)-20≤g(x)恒成立,则h(x)max≤-2在[0,2]恒成立.
h(x)的对称轴x=1−m2,
(1)若1−m2≤0即m≥1,h(x)在[0,2]递增,h(x)max=h(2)=4m-12≤-2,即m≤52,则1≤m≤52;
(2)若0<1−m2<2,即-3<m<1,
①若1−m2-0<2-1−m2,即m>-1,则h(x)max=h(2)=4m-12≤-2,即m≤52,故m∈(-1,1);
②若1−m2-0>2-1−m2,即m<-1,则h(x)max=h(0)=-4m-20≤-2,即m≥-92,故m∈[-92,-1);
③1−m2-0=2-1−m2,即m=-1,则h(x)max=h(0)=h(2)=4m-12=-4m-20,解得m=-1,即-16≤-2,故m=-1.
(3)若1−m2≥2,解得m≤-3,h(x)在[0,2]递减,则h(x)max=h(0)=-4m-20≤-2,解得m≥−92,
此时m∈[-92,-3].
综上可得,m的取值范围是[-92,52].
故答案为:[-92,52].
点评 本题考查不等式恒成立问题转化为求函数的最值问题,注意运用二次函数的对称轴和区间的关系,正确分类讨论是解题的关键.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | 10,-10 | B. | 20,-20 | C. | 30,20 | D. | 30,10 |
| A. | 1 | B. | √2 | C. | 2 | D. | 2√2 |
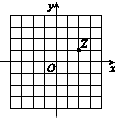 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数z1−2i的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数z1−2i的共轭复数是( )| A. | -35i | B. | -i | C. | 35i | D. | i |
| A. | 4√33 | B. | 2√3 | C. | 6 | D. | 4√3 |
 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.