题目内容
18.如图,O为圆心,若圆O的弦AB=3,弦AC=5,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是( )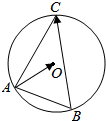
| A. | 1 | B. | 8 | C. | -1 | D. | -8 |
分析 如图所示,过点O作OD⊥BC交BC于点D,连接AD.则D为BC的中点,$\overrightarrow{OD}•\overrightarrow{BC}$=0.$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AB})$.又$\overrightarrow{AO}=\overrightarrow{AD}+\overrightarrow{DO}$,$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,即可得出.
解答 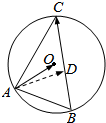 解:如图所示,过点O作OD⊥BC交BC于点D,连接AD.
解:如图所示,过点O作OD⊥BC交BC于点D,连接AD.
则D为BC的中点,$\overrightarrow{OD}•\overrightarrow{BC}$=0.
$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AB})$.又$\overrightarrow{AO}=\overrightarrow{AD}+\overrightarrow{DO}$,$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=($\overrightarrow{AD}+\overrightarrow{DO}$)$•\overrightarrow{BC}$=$\overrightarrow{AD}•\overrightarrow{BC}$=$\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AB})(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{1}{2}({\overrightarrow{AC}}^{2}-{\overrightarrow{AB}}^{2})$=$\frac{1}{2}({5}^{2}-{3}^{2})$=8;
故选:B.
点评 本题考查了三角形外心性质、向量是三角形法则、平行四边形法则、数量积运算,考查了推理能力与计算能力,属于难题

| A. | 必要条件 | B. | 充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
| A. | $x=-\frac{1}{16}$ | B. | $x=-\frac{1}{8}$ | C. | y=-1 | D. | y=-2 |
| A. | $\frac{13}{4}$或$\frac{7}{3}$ | B. | $\frac{16}{3}$或$\frac{8}{3}$ | C. | $\frac{13}{3}$ | D. | $\frac{16}{3}$ |
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |