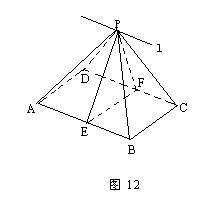
题目内容
如图,已知三棱锥A-BCD的侧视图,俯视图都是直角三角形,尺寸如图所示.
(1)求异面直线AB与CD所成角的余弦值;
(2)在线段AC上是否存在点F,使得BF⊥面ACD?若存在,求出CF的长度;若不存在说明理由.

(1)求异面直线AB与CD所成角的余弦值;
(2)在线段AC上是否存在点F,使得BF⊥面ACD?若存在,求出CF的长度;若不存在说明理由.

(1)取BD的中点O,连AO,则AO⊥面CBD.
以O为原点建立空间直角坐标系,如图.
A(0,0,1),B(1,0,0),C(1,2
,0),D(-1,0,0).
=(1,0,-1),
=(-2,-2
,0),cos<
,
>=-
.
所以所求异面直线AB与CD所成角的余弦值为
;(5分)
(2)设
=λ
,
则
=
+
=(-λ,2
(1-λ),λ)
由BF⊥面ACD得:
解得λ=
,
|
|=
|
|=
,(5分)
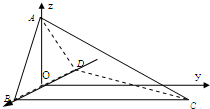
以O为原点建立空间直角坐标系,如图.
A(0,0,1),B(1,0,0),C(1,2
| 3 |
| AB |
| CD |
| 3 |
| AB |
| CD |
| ||
| 4 |
所以所求异面直线AB与CD所成角的余弦值为
| ||
| 4 |
(2)设
| CF |
| CA |
则
| BF |
| BC |
| CF |
| 3 |
由BF⊥面ACD得:
|
解得λ=
| 6 |
| 7 |
|
| CF |
| 6 |
| 7 |
| CA |
| 6 |
| 7 |
| 14 |


练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目