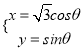题目内容
【题目】已知动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心的轨迹为曲线.
相内切,记圆心的轨迹为曲线.
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q为曲线C上的一个不在轴上的动点,O为坐标原点,过点![]() 作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由已知条件推导出|PF1|+|PF2|=8>|F1F2|=6,从而得到圆心P的轨迹为以F1,F2为焦点的椭圆,由此能求出圆心P的轨迹C的方程;(2)由MN∥OQ,知△QMN的面积=△OMN的面积,联立直线和椭圆得到二次方程,根据韦达定理和弦长公式得到△![]() 的面积
的面积![]() ,由此能求出△QMN的面积的最大值.
,由此能求出△QMN的面积的最大值.
解析:(Ⅰ)设圆的半径为, 圆心的坐标为![]() ,
,
由于动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,
相内切,
所以动圆与圆![]() 只能内切.
只能内切.
所以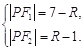
则![]() .
.
所以圆心的轨迹是以点![]() 为焦点的椭圆,
为焦点的椭圆,
且![]() , 则
, 则![]() .
.
所以曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由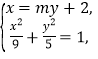 可得
可得![]() ,
,
则![]() .
.
所以![]()
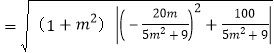
![]()
因为![]() ,所以△
,所以△![]() 的面积等于△
的面积等于△![]() 的面积.
的面积.
点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
所以△![]() 的面积
的面积![]() .
.
令![]() ,则
,则![]()
![]() ,
,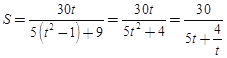 .
.
设![]() ,则
,则![]() .
.
因为![]() , 所以
, 所以![]()
所以![]() 在
在![]() 上单调递增.
上单调递增.
所以当![]() 时,
时, ![]() 取得最小值, 其值为
取得最小值, 其值为![]() .
.
所以△![]() 的面积的最大值为
的面积的最大值为![]() .
.
说明: △![]() 的面积
的面积![]() .
.

练习册系列答案
相关题目