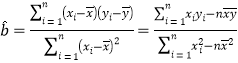题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() ,长轴长为
,长轴长为![]() ,
,![]() 为直线
为直线![]() :
:![]() 上的动点,
上的动点,![]() ,
,![]() .当
.当![]() 时,
时,![]() 与
与![]() 重合.
重合.
(1)若椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2) m=±1
(2) m=±1
【解析】试题分析:(1)根据题意得到由AF⊥BF得kAF·kBF=-1,进而求出椭圆方程;(2)由AP⊥AQ得,|AM|2=|PM|·|QM|,联立直线BM和椭圆得到二次方程,由韦达定理得到|PM|·|QM|的表达式,|AM|2=2+![]() ,两式相等即可.
,两式相等即可.
解析:
(Ⅰ)依题意得A(0,b),F(-c,0),当AB⊥l时,B(-3,b),
由AF⊥BF得kAF·kBF= ![]() ·
·![]() =-1,又b2+c2=6.
=-1,又b2+c2=6.
解得c=2,b=![]() .
.
所以,椭圆Γ的方程为![]() +
+![]() =1.
=1.
(Ⅱ)由(Ⅰ)得A(0,![]() ),依题意,显然m≠0,所以kAM=-
),依题意,显然m≠0,所以kAM=-![]() ,
,
又AM⊥BM,所以kBM=![]() ,所以直线BM的方程为y=
,所以直线BM的方程为y=![]() (x-m),
(x-m),
设P(x1,y1),Q(x2,y2).
y=![]() (x-m)与
(x-m)与![]() +
+![]() =1联立得(2+3m2)x2-6m3x+3m4-12=0,
=1联立得(2+3m2)x2-6m3x+3m4-12=0,
x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
|PM|·|QM|=(1+![]() )|(x1-m)(x2-m)|
)|(x1-m)(x2-m)|
=(1+![]() )|x1x2-m(x1+x2)+m2|
)|x1x2-m(x1+x2)+m2|
=(1+![]() )·
)·![]()
=![]() ,
,
|AM|2=2+m2,
由AP⊥AQ得,|AM|2=|PM|·|QM|,
所以![]() =1,解得m=±1.
=1,解得m=±1.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目