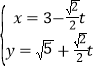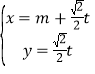题目内容
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
【答案】(1)直线![]() 的普通方程为
的普通方程为![]() ,圆
,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ)当![]() 时,消去
时,消去![]() 得到直线的普通方程,由圆
得到直线的普通方程,由圆![]() 极坐标方程,根据极坐标与直角坐标的互化公式,即可得到原的直角坐标方程.
极坐标方程,根据极坐标与直角坐标的互化公式,即可得到原的直角坐标方程.
(Ⅱ)将直线的参数方程代入圆的方程,![]() ,得
,得![]() ,由
,由![]() 的几何意义可求得
的几何意义可求得![]() 的值.
的值.
试题解析:
(Ⅰ)当![]() 时,
时,![]() 的参数方程为
的参数方程为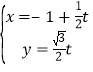 (
(![]() 为参数),
为参数),
消去![]() 得
得![]() .由圆
.由圆![]() 极坐标方程为
极坐标方程为![]() ,得
,得![]() .
.
故直线![]() 的普通方程为
的普通方程为![]() 圆
圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)将![]() 代入
代入![]() 得,
得,![]() .
.
设其两根分别为![]() ,则
,则![]() .
.
由![]() 的几何意义知
的几何意义知![]()
![]() .故
.故![]() 为定值
为定值![]() (与
(与![]() 无关) .
无关) .

练习册系列答案
相关题目
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.