题目内容
在四棱锥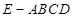 中,底面
中,底面 是正方形,
是正方形,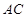 与
与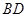 交于点
交于点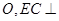 底面
底面 ,
,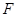 为
为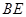 的中点.
的中点.
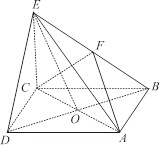
(1)求证: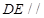 平面
平面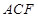 ;
;
(2)若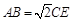 ,在线段
,在线段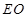 上是否存在点
上是否存在点 ,使
,使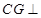 平面
平面 ?若存在,求出
?若存在,求出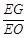 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
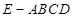 中,底面
中,底面 是正方形,
是正方形,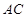 与
与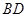 交于点
交于点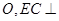 底面
底面 ,
,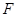 为
为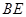 的中点.
的中点.
(1)求证:
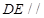 平面
平面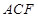 ;
;(2)若
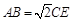 ,在线段
,在线段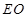 上是否存在点
上是否存在点 ,使
,使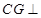 平面
平面 ?若存在,求出
?若存在,求出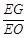 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)详见解析;(2) 为线段
为线段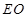 的中点时,
的中点时,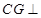 平面
平面 ,理由详见解析.
,理由详见解析.
 为线段
为线段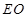 的中点时,
的中点时,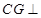 平面
平面 ,理由详见解析.
,理由详见解析.试题分析:(1)利用三角形的中位线定理证明
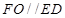 ,然后根据线面平行的判定定理进行证明即可;(2)这是存在性问题,先假设存在点
,然后根据线面平行的判定定理进行证明即可;(2)这是存在性问题,先假设存在点 ,使得
,使得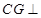 平面
平面 ,依据面面垂直的判定定理可知,这时必有面
,依据面面垂直的判定定理可知,这时必有面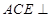 面
面 ,此时应该在平面
,此时应该在平面 中可以找到一条直线垂直平面
中可以找到一条直线垂直平面 ,这时关注好题目中的条件:底面
,这时关注好题目中的条件:底面 为正方形且
为正方形且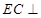 面
面 ,此时可想到可能是
,此时可想到可能是 面
面 ,这个垂直关系并不难证明,故可肯定点
,这个垂直关系并不难证明,故可肯定点 是存在的,然后再根据题中所给的条件去确定边
是存在的,然后再根据题中所给的条件去确定边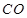 与
与 的比例关系,最后根据
的比例关系,最后根据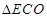 为直角三角形且
为直角三角形且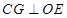 可确定
可确定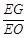 的比值.
的比值.试题解析:(1)证明:连接
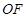
由四边形
 是正方形可知,点
是正方形可知,点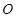 为
为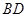 的中点
的中点又
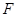 为
为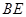 的中点,所以
的中点,所以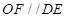
又
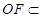 平面
平面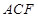 ,
,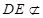 平面
平面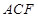
所以
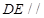 平面
平面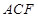 6分
6分(2)解法一:若
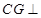 平面
平面 ,则必有
,则必有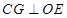
于是作
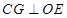 于点
于点
由
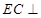 底面
底面 ,所以
,所以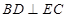 ,又底面
,又底面 是正方形
是正方形所以
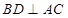 ,又
,又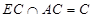 ,所以
,所以 平面
平面 10分
10分而
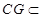 平面
平面 ,所以
,所以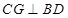
又
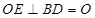 ,所以
,所以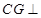 平面
平面 12分
12分又
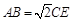 ,所以
,所以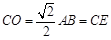
所以
 为
为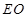 的中点,所以
的中点,所以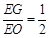 14分
14分解法二:取
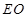 的中点
的中点 ,连接
,连接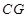 ,在四棱锥
,在四棱锥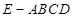 中
中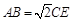 ,
,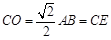 ,所以
,所以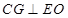 6分
6分又由
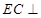 底面
底面 ,
,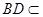 底面
底面 ,所以
,所以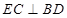
由四边形
 是正方形可知,
是正方形可知,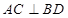
又
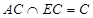
所以
 平面
平面 10分
10分而
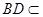 平面
平面
所以,平面
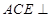 平面
平面 ,且平面
,且平面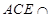 平面
平面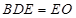
因为
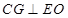 ,
,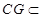 平面
平面 ,所以
,所以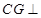 平面
平面 12分
12分故在线段
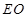 上存在点
上存在点 ,使
,使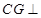 平面
平面
由
 为
为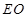 的中点,得
的中点,得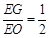 14分.
14分.
练习册系列答案
相关题目

 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度. 中,点
中,点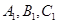 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且 ,E为
,E为 中点,
中点, .
.
 ,
, 平面
平面
 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
 平面
平面 ;
; 平面
平面 .
.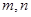 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( ) 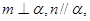 则
则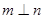
 则
则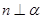
 则
则
 ,则
,则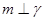
 //平面
//平面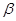 ,
,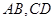 是夹在
是夹在 间的线段,若
间的线段,若 //
//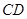 ,则
,则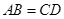 ;
; 是异面直线,
是异面直线,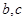 是异面直线,则
是异面直线,则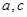 一定是异面直线;
一定是异面直线;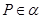 ,
, //
//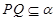 ;
; 、
、 是不同的直线,
是不同的直线, 、
、 是不同的平面,则下列命题:
是不同的平面,则下列命题: ,则
,则 ;②若
;②若 ,则
,则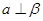 ;
; ,则
,则 ;④若
;④若 ,则
,则 .
.