题目内容
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.

(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=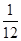 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.

(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=
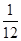 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.(1)见解析(2)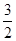
(1)证明:∵AA1=A1C=AC=2,且O为AC中点,
∴A1O⊥AC,又∵侧面AA1C1C⊥底面ABC,侧面AA1C1C∩底面ABC=AC,A1O?平面A1AC,
∴A1O⊥平面ABC.
(2)∵VE-BCC1=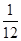 VABC-A1B1C1=
VABC-A1B1C1=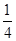 VA1-BCC1,∴BE=
VA1-BCC1,∴BE=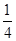 BA1,即A1E=
BA1,即A1E=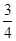 A1B.
A1B.
连接OB,在Rt△A1OB中,A1O⊥OB,A1O=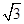 ,BO=1,故A1B=2,则A1E的长度为
,BO=1,故A1B=2,则A1E的长度为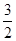 .
.
∴A1O⊥AC,又∵侧面AA1C1C⊥底面ABC,侧面AA1C1C∩底面ABC=AC,A1O?平面A1AC,
∴A1O⊥平面ABC.
(2)∵VE-BCC1=
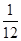 VABC-A1B1C1=
VABC-A1B1C1=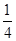 VA1-BCC1,∴BE=
VA1-BCC1,∴BE=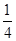 BA1,即A1E=
BA1,即A1E=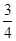 A1B.
A1B.连接OB,在Rt△A1OB中,A1O⊥OB,A1O=
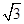 ,BO=1,故A1B=2,则A1E的长度为
,BO=1,故A1B=2,则A1E的长度为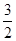 .
.
练习册系列答案
相关题目

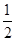 AB.直角梯形ACEF中,
AB.直角梯形ACEF中,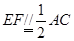 ,
,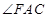 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.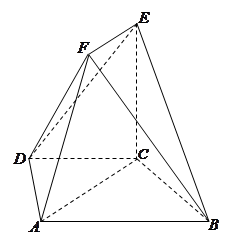
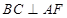 ;
;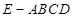 中,底面
中,底面 是正方形,
是正方形,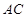 与
与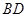 交于点
交于点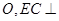 底面
底面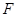 为
为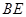 的中点.
的中点.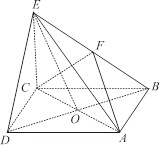
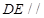 平面
平面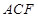 ;
;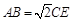 ,在线段
,在线段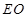 上是否存在点
上是否存在点 ,使
,使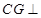 平面
平面 ?若存在,求出
?若存在,求出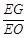 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.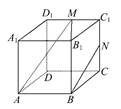
 ,直线
,直线 ,且有
,且有 ,则下列四个命题正确的个数为( )
,则下列四个命题正确的个数为( ) ∥
∥ 则
则 ;②若
;②若 ∥
∥ 则
则 则
则 ;
;


