题目内容
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,则这个定值为
的等边三角形内任一点到三边距离之和为定值,则这个定值为![]() ;推广到空间,棱长为
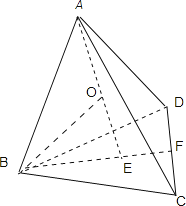
;推广到空间,棱长为![]() 的正四面体内任一点到各面距离之和为___________________.
的正四面体内任一点到各面距离之和为___________________.
【答案】![]()
【解析】
由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.固我们可以根据已知中平面几何中,关于线的性质“正三角形内任意一点到三边距离之和是一个定值”,推断出一个空间几何中一个关于面的性质
在边长为![]() 的正三角形内任一点到三边的距离之和为定值
的正三角形内任一点到三边的距离之和为定值![]() ,
,
在一个正四面体中,计算一下棱长为![]() 的三棱锥内任一点到各个面的距离之和,由棱长为
的三棱锥内任一点到各个面的距离之和,由棱长为![]() 可以得到
可以得到![]()
![]() ,
,
在直角三角形中,根据勾股定理可以得到![]() ,
,
把数据代入得到![]() ,
,![]() 棱长为
棱长为![]() 的三棱锥内任一点到各个面的距离之和
的三棱锥内任一点到各个面的距离之和![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?