题目内容
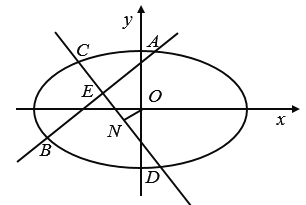
【题目】已知椭圆E:![]() ,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
![]() 若
若![]() ,点K在椭圆E上,
,点K在椭圆E上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
![]() 证明:直线OM的斜率与l的斜率的乘积为定值;
证明:直线OM的斜率与l的斜率的乘积为定值;
![]() 若l过点
若l过点![]() ,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
【答案】(1)![]() (2)见证明;(3)见解析
(2)见证明;(3)见解析
【解析】
![]() ,椭圆E:
,椭圆E:![]() ,两个焦点
,两个焦点![]() ,
,![]() ,设
,设![]() ,求出
,求出![]() 的表达式,然后求解范围即可.
的表达式,然后求解范围即可.![]() 设A,B的坐标分别为
设A,B的坐标分别为![]() ,
,![]() ,利用点差法转化求解即可.
,利用点差法转化求解即可.![]() 直线l过点
直线l过点![]() ,直线l不过原点且与椭圆E有两个交点的充要条件是
,直线l不过原点且与椭圆E有两个交点的充要条件是![]() 且
且![]() 设
设![]() ,设直线
,设直线![]() ,代入椭圆方程,通过四边形OAPB为平行四边形,转化求解即可.
,代入椭圆方程,通过四边形OAPB为平行四边形,转化求解即可.
![]() ,椭圆E:
,椭圆E:![]() ,两个焦点
,两个焦点![]() ,
,![]()
设![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的范围是
的范围是![]()
![]() 设A,B的坐标分别为
设A,B的坐标分别为![]() ,
,![]() ,则
,则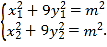 两式相减,
两式相减,
得![]() ,
,![]() ,
,
即![]() ,故
,故![]() ;
;
![]() 设
设![]() ,设直线
,设直线![]() ,即
,即![]() ,
,
由![]() 的结论可知
的结论可知![]() ,代入椭圆方程得,
,代入椭圆方程得,![]() ,
,
由![]() 与
与![]() ,联立得
,联立得![]()
若四边形OAPB为平行四边形,那么M也是OP的中点,所以![]() ,
,
即![]() ,整理得
,整理得![]() 解得,
解得,![]() .经检验满足题意
.经检验满足题意
所以当![]() 时,四边形OAPB为平行四边形
时,四边形OAPB为平行四边形![]()

练习册系列答案
相关题目