[题目]设等差数列{an}的公差d＞0.前n项和为Sn . 已知3 是﹣a2与a9的等比中项.S10=﹣20．(1)求数列{an}的通项公式,(2)设bn= .求数列{bn}的前n项和Tn．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设等差数列{an}的公差d＞0，前n项和为Sn ，已知3 是﹣a2与a9的等比中项，S10=﹣20．
（1）求数列{an}的通项公式；
（2）设bn= ，求数列{bn}的前n项和Tn（n≥6）．

【答案】
（1）解：∵3 是﹣a2与a9的等比中项，∴ =﹣a2a9，又S10=﹣20．

∴﹣（a1+d）（a1+8d）=45，10a1+ d=﹣20，

联立解得a1=﹣11，d=2．

∴an=﹣11+2（n﹣1）=2n﹣13

（2）解：1≤n≤5时，bn= = =﹣ ．

n≥6，bn= = = ，

∴n≥6时，数列{bn}的前n项和Tn=﹣ +

= ﹣

【解析】（1）利用等比数列的通项公式与性质、等差数列的通项公式与求和公式即可得出．（2）分类讨论，利用“裂项求和”方法即可得出．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系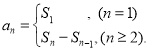；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．

练习册系列答案

相关题目

【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点．研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度（单位：千克/年）是养殖密度（单位：尾/立方米）的函数．当不超过尾/立方米时，的值为千克/年；当时，是的一次函数，且当时，．

（）当时，求关于的函数的表达式．

（）当养殖密度为多大时，每立方米的鱼的年生长量（单位：千克/立方米）可以达到最大？并求出最大值．

【题目】关于f(x)＝4sin (x∈R)，有下列命题

①由f(x1)＝f(x2)＝0可得x1－x2是π的整数倍；

②y＝f(x)的表达式可改写成y＝4cos；

③y＝f(x)图象关于对称；

④y＝f(x)图象关于x＝－对称．

其中正确命题的序号为________(将你认为正确的都填上)。

【题目】已知的一个顶点为抛物线的顶点，，两点都在抛物线上，且.

（1）求证：直线必过一定点；

（2）求证：面积的最小值.

【题目】在△ABC中，D、E是BC边上两点，BD、BA、BC构成以2为公比的等比数列，BD=6，∠AEB=2∠BAD，AE=9，则三角形ADE的面积为（）
A.31.2
B.32.4
C.33.6
D.34.8

【题目】某某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：，并整理得到如下频率分布直方图：

（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；

（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；

（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

【题目】《最强大脑》是江苏卫视推出国内首档大型科学类真人秀电视节目，该节目集结了国内外最顶尖的脑力高手，堪称脑力界的奥林匹克，某校为了增强学生的记忆力和辨识力也组织了一场类似《最强大脑》的PK赛，A、B两队各由4名选手组成，每局两队各派一名选手PK，除第三局胜者得2分外，其余各局胜者均得1分，每局的负者得0分，假设每局比赛两队选手获胜的概率均为0.5，且各局比赛结果相互独立．
（1）求比赛结束时A队的得分高于B队的得分的概率；
（2）求比赛结束时B队得分X的分布列和期望．

【题目】对于函数，若，则称为的“不动点”；若，则称为的“稳定点”．函数的“不动点”和“稳定点”的集合分别记为和，即，．