[题目]如图.在直三棱柱中.,,,分别为棱的中点．(1)求证:∥平面(2)若异面直线与所成角为.求三棱锥的体积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在直三棱柱中，,,,分别为棱的中点．

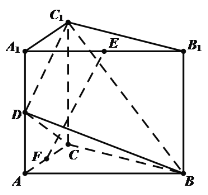
（1）求证:∥平面

（2）若异面直线与所成角为，求三棱锥的体积．

【答案】（1）见解析；（2）

【解析】

分析：（1）取的中点,连接, ，由棱柱的性质可得∥,∥,，再由面面平行的判定得到平面平面∥平面，，则答案得到证明；
（2）由（1）知知异面直线与所成角,所以, ，进一步得到平面,,，再由已知求出的长度，把三棱锥的体积转化为的体积求解．

详解：

（1）证明：取的中点,连接,

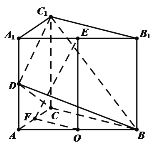
因为分别为棱的中点，所以∥,∥,，

，同理可证，且,平面,

所以平面∥平面，

又平面,所以∥平面.

（2）由（1）知异面直线与所成角,所以,

因为三棱柱为直三棱柱，所以平面,所以平面,

,又,,

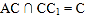,,平面,

所以 .

练习册系列答案

相关题目

【题目】设等差数列{an}的公差d＞0，前n项和为Sn ，已知3 是﹣a2与a9的等比中项，S10=﹣20．
（1）求数列{an}的通项公式；
（2）设bn= ，求数列{bn}的前n项和Tn（n≥6）．

【题目】已知是方程的两根, 数列是公差为正的等差数列，数列的前项和为,且.

(1)求数列的通项公式；

(2)记,求数列的前项和.

【题目】对于n∈N* ，若数列{xn}满足xn+1﹣xn＞1，则称这个数列为“K数列”．
（Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数m的取值范围；
（Ⅱ）是否存在首项为﹣1的等差数列{an}为“K数列”，且其前n项和Sn满足？若存在，求出{an}的通项公式；若不存在，请说明理由；
（Ⅲ）已知各项均为正整数的等比数列{an}是“K数列”，数列不是“K数列”，若，试判断数列{bn}是否为“K数列”，并说明理由．