题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点. 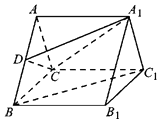
(Ⅰ)若BC1∥平面A1CD,确定D的位置,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求二面角A1D﹣C﹣BC1的余弦值.
【答案】解:(Ⅰ)D为AB的中点,理由如下:
连接AC1,交A1C于点E,可知E为AC1的中点,连接DE,
因为BC1∥平面A1CD,
平面ABC1∩平面A1CD=DE,
所以BC1∥DE,
故D为AB的中点.
(Ⅱ)不妨设AB=2,分别取BC,B1C1的中点O,O1,连接AO,OO1,可知OB,OO1,OA两两互相垂直,建立如图的空间直角坐标系O﹣xyz.
知 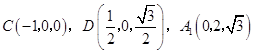 ,
,
则 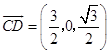 ,
, ![]() ,
,
设面A1CD的法向量m=(x,y,z),
由 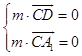 得
得 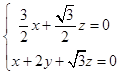
令x=1,得A1CD的一个法向量为 ![]() ,
,
又平面BCC1的一个法向量n=(0,0,1),
设二面角A1D﹣C﹣BC1的平面角为α,
则 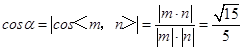 .
.
即该二面角的余弦值为 ![]() .
.
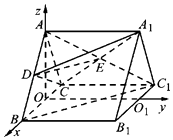
【解析】(Ⅰ)D为AB的中点,理由如下:连接AC1,交A1C于点E,可知E为AC1的中点,连接DE,利用线面平行的性质定理、三角形中平行线的性质即可得出.(Ⅱ)不妨设AB=2,分别取BC,B1C1的中点O,O1,连接AO,OO1,可知OB,OO1,OA两两互相垂直,建立如图的空间直角坐标系O﹣xyz.利用线面垂直的性质定理、向量垂直与数量积的关系可得:平面A1CD的法向量 ![]() ,又平面BCC1的一个法向量
,又平面BCC1的一个法向量 ![]() =(0,0,1),利用向量夹角公式即可得出.
=(0,0,1),利用向量夹角公式即可得出.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应关系:
x/百万元 | 2 | 4 | 5 | 6 | 8 |
y/百万元 | 30 | 40 | 60 | 50 | 70 |
(1)假定y与x之间有线性相关关系,求其回归直线方程;
(2)若实际的销售额不少于60百万元,则广告费支出应不少于多少?