题目内容
一个袋中装有形状大小完全相同的球9个,其中红球3个,白球6个,每次随机取1个,直到取出3次红球即停止.
(1)从袋中不放回地取球,求恰好取4次停止的概率P1;
(2)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为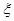 ,求随机变量
,求随机变量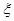 的分布列及数学期望.
的分布列及数学期望.
(1)从袋中不放回地取球,求恰好取4次停止的概率P1;
(2)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为
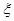 ,求随机变量
,求随机变量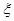 的分布列及数学期望.
的分布列及数学期望.(1)  (2) ①
(2) ① ②
②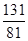
 (2) ①
(2) ① ②
②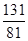
试题分析:(1)从袋中不放回地取球,连续取4次,有
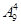 个不同的结果,由于是随机取的,每个结果出现的可能性是相等的,恰好取4次停止,说明前三次有一次是白球,共有
个不同的结果,由于是随机取的,每个结果出现的可能性是相等的,恰好取4次停止,说明前三次有一次是白球,共有 个不同的结果,所以,根据古典概型的概率公式得
个不同的结果,所以,根据古典概型的概率公式得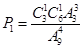 ;
;(2) 从袋中有放回地取球,每次取到红球的概率
 ,取到白球的概率是
,取到白球的概率是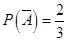 连续有放回地取
连续有放回地取 次,相当于
次,相当于 次独立重复试验;
次独立重复试验; ①求恰好取5次停止的概率P2;说明前四次有两次发生,第五次一定发生;
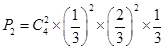
②记5次之内(含5次)取到红球的个数为
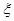 ,随机变量
,随机变量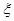 的所以可能取值集合是
的所以可能取值集合是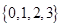
由
 次独立重复试验概率公式
次独立重复试验概率公式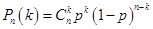 即可求出随机变量
即可求出随机变量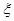 分布列,并由数学期望的公式计算出
分布列,并由数学期望的公式计算出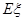 .
.试题解析:
解:(1)
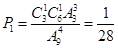 4分
4分(2)①
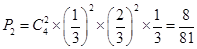 6分
6分②随机变量
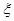 的取值为
的取值为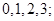
由
 次独立重复试验概率公式
次独立重复试验概率公式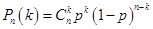 ,得
,得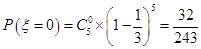
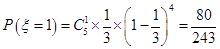
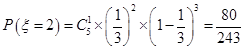

随机变量
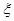 的分布列是
的分布列是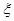 | 0 | 1 | 2 | 3 |
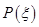 |  | 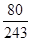 | 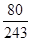 | 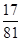 |
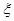 的数学期望是
的数学期望是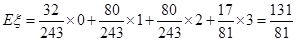 12分
12分
练习册系列答案
相关题目
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:












 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生? 的概率.
的概率. ,求
,求 ,从中任取三个数,则至少有两个数位于同行或同列的概率是____________. (结果用分数表示)
,从中任取三个数,则至少有两个数位于同行或同列的概率是____________. (结果用分数表示)



