题目内容
(本小题满分9分)一个袋子中有3个红球和2个黄球,5个球除颜色外完全相同,甲、乙两人先后不放回地从中各取1个球.规定:若两人取得的球的颜色相同则甲获胜,否则乙获胜.
(1) 求两个人都取到黄球的概率;
(2) 计算甲获胜的概率.
(1) 求两个人都取到黄球的概率;
(2) 计算甲获胜的概率.
(1) ;(2)
;(2)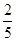 .
.
 ;(2)
;(2)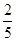 .
.试题分析:(1) 设3个红球编号为1、2、3;两个黄球编号为4、5,分别列出甲乙两人先后不放回地各取一个球的所有基本事件
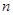 ,然后找到其中的两人都取到黄球的事件
,然后找到其中的两人都取到黄球的事件 ,
,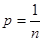 ;
;(2)甲获胜指的是两人取到相同颜色的球,即两个红的或是两个黄的.看其中有几个基本事件
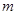 ,
,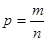 .
.解:设3个红球编号为1、2、3;两个黄球编号为4、5.则一切可能结果组成的基本事件有(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)共10个。 (2分)
两个人都取得黄球的事件有(4,5)共1个。因此两个人都取得黄球概率为P=

(6分(注意格式,要设事件,要作答))
(2)两个人取得相同颜色球的事件有(1,2)、(1,3)、(2,3)、(4,5)共4个
故甲获胜的概率为P=
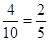 . (9分(注意格式,要设事件,要作答))
. (9分(注意格式,要设事件,要作答))
练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
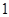 的球
的球 个,编号为
个,编号为 的球
的球 个,这些球的大小完全一样。
个,这些球的大小完全一样。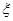 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量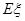 .
.
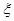 ,求随机变量
,求随机变量 .
.