题目内容
某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1,2,3,4,5名,“二检”中的前5名依然是这五名同学.
(1)求恰好有两名同学排名不变的概率;
(2)如果设同学排名不变的同学人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1)求恰好有两名同学排名不变的概率;
(2)如果设同学排名不变的同学人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(1)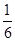 ;(2)
;(2) 分布列为
分布列为
 的数学期望
的数学期望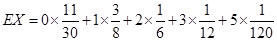
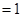 .
.
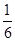 ;(2)
;(2) 分布列为
分布列为 | 0 | 1 | 2 | 3 | 5 |
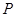 | 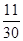 | 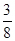 | 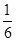 |  | 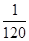 |
 的数学期望
的数学期望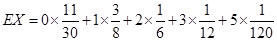
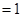 .
.试题分析:(1)第二次排名的基本事件总数为
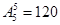 ,恰有2名同学排名不变所包含的基本事件数有:
,恰有2名同学排名不变所包含的基本事件数有: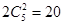 种(先确定哪两个同学的排名不变,排名变化的三名同学只有两种情况),从而根据古典概型的概率计算公式即可求得所求的概率;(2)先确定
种(先确定哪两个同学的排名不变,排名变化的三名同学只有两种情况),从而根据古典概型的概率计算公式即可求得所求的概率;(2)先确定 所有可能的取值
所有可能的取值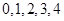 ,再分别求解
,再分别求解 时的概率,方法与(1)同,仍属古典概率问题,最后再根据概率和为1计算出
时的概率,方法与(1)同,仍属古典概率问题,最后再根据概率和为1计算出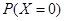 ,进而列出分布列,根据期望的计算公式计算出期望即可.
,进而列出分布列,根据期望的计算公式计算出期望即可.(1)第二次排名,恰好有两名同学排名不变的情况数为:
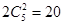 (种)
(种)第二次排名情况总数为:
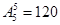 ,所以恰好有两名同学排名不变的概率为
,所以恰好有两名同学排名不变的概率为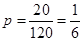
(2)第二次同学排名不变的同学人数
 可能的取值为:5,3,2,1,0
可能的取值为:5,3,2,1,0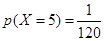

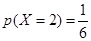
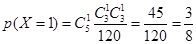
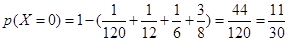
 分布列为
分布列为 | 0 | 1 | 2 | 3 | 5 |
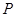 | 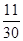 | 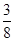 | 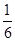 | 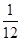 | 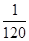 |
 的数学期望
的数学期望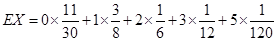
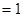 12分.
12分.
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
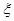 ,求随机变量
,求随机变量 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
 ,则至少得到1个白球的概率是 .
,则至少得到1个白球的概率是 . ,
, ,其中
,其中 记“使得
记“使得 成立的
成立的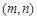 ”为事件A,则事件A发生的概率为( )
”为事件A,则事件A发生的概率为( )



 ,身体关节构造合格的概率为
,身体关节构造合格的概率为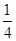 ,从中任挑一儿童,这两项至少有一项合格的概率是________(假定体型与身体关节构造合格与否相互之间没有影响).
,从中任挑一儿童,这两项至少有一项合格的概率是________(假定体型与身体关节构造合格与否相互之间没有影响).