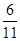题目内容
某校高三(1)班共有 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:
(1)求分布表中 ,
, 的值;
的值;
(2)王老师为完成一项研究,按学习时间用分层抽样的方法从这 名学生中抽取
名学生中抽取 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?
(3)已知第一组学生中男、女生人数相同,在(2)的条件下抽取的第一组学生中,既有男生又有女生的概率是多少?
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表:| 组别 | 分组 | 频数 | 频率 |
| 第一组 |  | |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  |  |  |
| 第五组 |  | |  |
 ,
, 的值;
的值;(2)王老师为完成一项研究,按学习时间用分层抽样的方法从这
 名学生中抽取
名学生中抽取 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?(3)已知第一组学生中男、女生人数相同,在(2)的条件下抽取的第一组学生中,既有男生又有女生的概率是多少?
(1)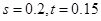 (2)
(2)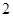 (3)
(3)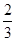
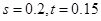 (2)
(2)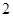 (3)
(3)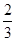
试题分析:
(1)第二组的频数已知,则根据根据频率的计算公式(频率=频数除以总数)即可得到频率s,再利用各组频率之和为1,即可计算得到第五组的频率t.
(2)根据抽样的原理,即在抽样过程中,保持每个个体被抽到的可能性相同,则要在40人中抽去20人,即抽取的比列为0.5,在第一组学生中抽取的比列也为0.5,即需要2人.
(3)由(2)可以知道为4选2,首先对4个人进行编号,然后列出4抽2的所有的基本事件,并计算得到满足抽取的两个人一个为女生,一个为男生的基本事件数,根据古典概型的概率计算公式即可得到相应的概率.
试题解析:
(1)
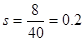 ,
,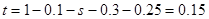 . 4分
. 4分(2)设应抽取
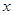 名第一组的学生,则
名第一组的学生,则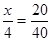
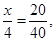 得
得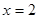 .
.故应抽取2名第一组的学生. 6分
(3)在(2)的条件下应抽取2名第一组的学生,记第一组中2名男生为
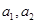 ,2名女生为
,2名女生为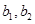 .
.按时间用分层抽样的方法抽取2名第一组的学生共有
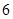 种结果,列举如下:
种结果,列举如下: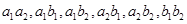 . 9分
. 9分其中既有男生又有女生被抽中的有
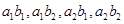 这4种结果, 10分
这4种结果, 10分所以既有男生又有女生被抽中的概率为
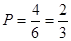 . 12分
. 12分
练习册系列答案
相关题目
 ,求随机变量
,求随机变量 ,则至少得到1个白球的概率是 .
,则至少得到1个白球的概率是 .



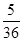
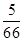
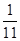
 ,则
,则 的概率为( )
的概率为( )