题目内容
已知a、b、c成等比数列，如果a、x、b和b、y、c都成等差数列，则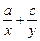
=_________
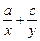=_________ 2
解法一: 赋值法.
解法二:b=aq,c=aq2,x=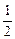
(a+b)=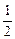a(1+q),y=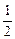(b+c)=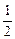aq(1+q),
=
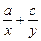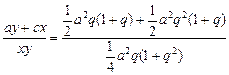=2.
解法二:b=aq,c=aq2,x=
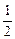(a+b)=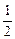a(1+q),y=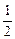(b+c)=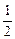aq(1+q), 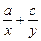==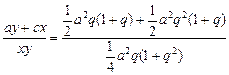2.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
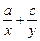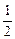=_________ (a+b)=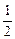a(1+q),y=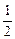(b+c)=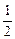aq(1+q), 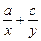==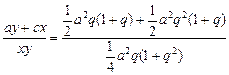2.阅读快车系列答案
的通项公式为
．
是否是数列
，求
．
满足：对于
都有
求
（2）若
求
求
取哪些值时，无穷数列
(n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m，使得对任意n∈N*均有Tn＞
成立？若存在，求出m的值；若不存在，说明理由.
，其中Sn=b1+b2+…+bn；
，求数列{
}的最大项和最小项的值. 
)x(0<a<1)的图像上，且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形. 
中，
为
的两个根，则
.