题目内容
已知数列 满足:对于
满足:对于 都有
都有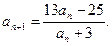
(1)若 求
求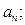 (2)若
(2)若 求
求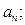 (3)若
(3)若 求
求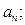
(4)当 取哪些值时,无穷数列
取哪些值时,无穷数列 不存在?
不存在?
 满足:对于
满足:对于 都有
都有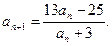
(1)若
 求
求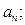 (2)若
(2)若 求
求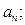 (3)若
(3)若 求
求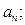
(4)当
 取哪些值时,无穷数列
取哪些值时,无穷数列 不存在?
不存在?(1)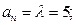 (2)
(2) (3)
(3) (4)数列
(4)数列 从第
从第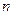 项开始便不存在
项开始便不存在
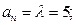 (2)
(2) (3)
(3) (4)数列
(4)数列 从第
从第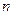 项开始便不存在
项开始便不存在作特征方程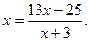 变形得
变形得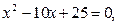
特征方程有两个相同的特征根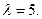 依定理2的第(1)部分解答.
依定理2的第(1)部分解答.
(1)∵ 对于
对于 都有
都有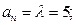
(2)∵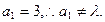
∴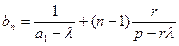
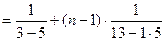
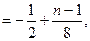
令 ,得
,得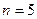 .故数列
.故数列 从第5项开始都不存在,
从第5项开始都不存在,
当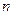 ≤4,
≤4, 时,
时, .
.
(3)∵ ∴
∴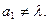
∴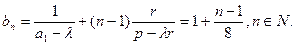
令 则
则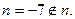 ∴对于
∴对于
∴
(4)、显然当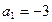 时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知,
时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知, 时,数列
时,数列 是存在的,当
是存在的,当 时,则有
时,则有 令
令 则得
则得 且
且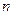 ≥2.
≥2.
∴当 (其中
(其中 且N≥2)时,数列
且N≥2)时,数列 从第
从第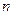 项开始便不存在.
项开始便不存在.
于是知:当 在集合
在集合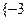 或
或 且
且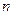 ≥2}上取值时,无穷数列
≥2}上取值时,无穷数列 都不存在.
都不存在.
说明:形如: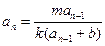 递推式,考虑函数倒数关系有
递推式,考虑函数倒数关系有

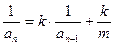 令
令 则
则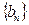 可归为
可归为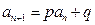 型。(取倒数法)
型。(取倒数法)
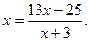 变形得
变形得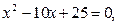
特征方程有两个相同的特征根
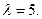 依定理2的第(1)部分解答.
依定理2的第(1)部分解答.(1)∵
 对于
对于 都有
都有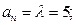
(2)∵
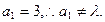
∴
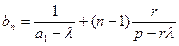
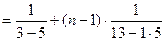
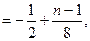
令
 ,得
,得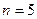 .故数列
.故数列 从第5项开始都不存在,
从第5项开始都不存在,当
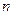 ≤4,
≤4, 时,
时, .
.(3)∵
 ∴
∴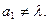
∴
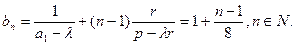
令
 则
则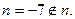 ∴对于
∴对于
∴

(4)、显然当
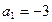 时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知,
时,数列从第2项开始便不存在.由本题的第(1)小题的解答过程知, 时,数列
时,数列 是存在的,当
是存在的,当 时,则有
时,则有 令
令 则得
则得 且
且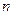 ≥2.
≥2.∴当
 (其中
(其中 且N≥2)时,数列
且N≥2)时,数列 从第
从第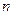 项开始便不存在.
项开始便不存在.于是知:当
 在集合
在集合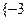 或
或 且
且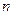 ≥2}上取值时,无穷数列
≥2}上取值时,无穷数列 都不存在.
都不存在.说明:形如:
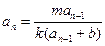 递推式,考虑函数倒数关系有
递推式,考虑函数倒数关系有

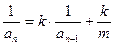 令
令 则
则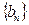 可归为
可归为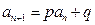 型。(取倒数法)
型。(取倒数法)
练习册系列答案
相关题目
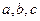 不全相等.
不全相等.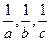 能构成等差数列吗?你能用函数图象解释一下吗?
能构成等差数列吗?你能用函数图象解释一下吗?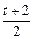 处取得最小值-
处取得最小值-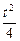 (t>0),f(1)=0.
(t>0),f(1)=0.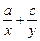 =_________
=_________
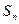 为等差数列
为等差数列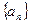 的前
的前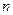 项和,
项和,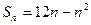 .
.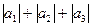 ;
; 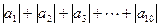 ;
;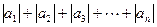 .
.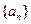 中,已知
中,已知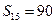 ,那么
,那么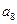 等于
等于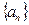 中,
中,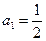 ,前n项的和
,前n项的和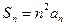 ,求
,求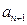 .
.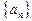 中
中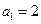 ,点
,点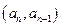 在函数
在函数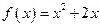 的图
的图 像上
像上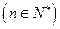 ,(1)求
,(1)求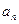 ,(2)若
,(2)若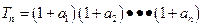 ,求
,求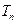 .
.