题目内容
在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,对每个自然数n点Pn位于函数y=2000(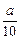 )x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
(1)求点Pn的纵坐标bn的表达式;
(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由.
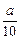 )x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形. (1)求点Pn的纵坐标bn的表达式;
(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由.
(1) bn=2000(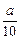 )
)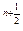 ,(2) 5(
,(2) 5(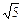 -1)<a<10, (3)前20项
-1)<a<10, (3)前20项
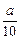 )
)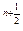 ,(2) 5(
,(2) 5(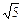 -1)<a<10, (3)前20项
-1)<a<10, (3)前20项(1)由题意知:an=n+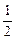 ,∴bn=2000(
,∴bn=2000(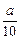 )
)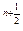 .
.
(2)∵函数y=2000(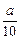 )x(0<a<10)递减,
)x(0<a<10)递减,
∴对每个自然数n,有bn>bn+1>bn+2.
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即(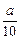 )2+(
)2+(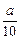 )-1>0,
)-1>0,
解得a<-5(1+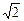 )或a>5(
)或a>5(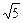 -1)
-1) ∴5(
∴5(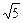 -1)<a<10.
-1)<a<10.
(3)∵5(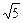 -1)<a<10,∴a=7
-1)<a<10,∴a=7
∴bn=2000(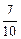 )
)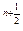
 数列{bn}是一个递减的正数数列,
数列{bn}是一个递减的正数数列,
对每个自然数n≥2,Bn=bnBn-1.
于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
因此数列{Bn}的最大项的项数n满足不等式bn≥1且bn+1<1,
由bn=2000(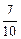 )
)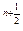 ≥1得: n≤20.8. ∴n=20.
≥1得: n≤20.8. ∴n=20.
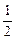 ,∴bn=2000(
,∴bn=2000(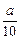 )
)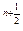 .
.(2)∵函数y=2000(
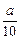 )x(0<a<10)递减,
)x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2.
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即(
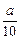 )2+(
)2+(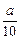 )-1>0,
)-1>0,解得a<-5(1+
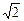 )或a>5(
)或a>5(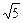 -1)
-1) ∴5(
∴5(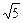 -1)<a<10.
-1)<a<10.(3)∵5(
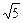 -1)<a<10,∴a=7
-1)<a<10,∴a=7∴bn=2000(
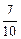 )
)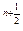
 数列{bn}是一个递减的正数数列,
数列{bn}是一个递减的正数数列,对每个自然数n≥2,Bn=bnBn-1.
于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
因此数列{Bn}的最大项的项数n满足不等式bn≥1且bn+1<1,
由bn=2000(
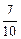 )
)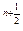 ≥1得: n≤20.8. ∴n=20.
≥1得: n≤20.8. ∴n=20.
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
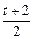 处取得最小值-
处取得最小值-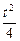 (t>0),f(1)=0.
(t>0),f(1)=0.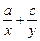 =_________
=_________
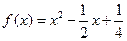 ,
,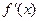 为函数
为函数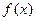 的导函数.
的导函数.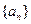 满足:
满足: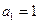 ,
,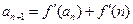 (
(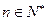 ),求数列
),求数列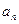 ;
;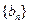 满足:
满足: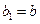 ,
,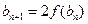 (
(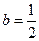 时,数列
时,数列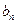 ;若不是,请说明理由;
;若不是,请说明理由;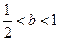 时, 求证:
时, 求证: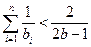 .
.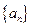 满足
满足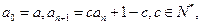 其中
其中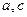 为实数,且
为实数,且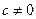
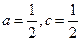 ,
,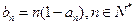 ,求数列
,求数列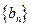 的前
的前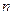 项和
项和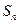 ;
;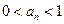 对任意
对任意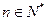 成立,证明
成立,证明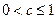
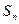 为等差数列
为等差数列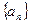 的前
的前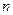 项和,
项和,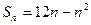 .
.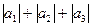 ;
; 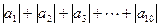 ;
;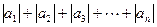 .
.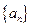 中,
中,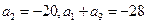 .
.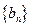 满足
满足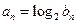 ,设
,设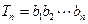 ,且
,且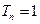 ,求
,求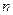 的值.
的值.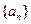 中,已知
中,已知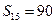 ,那么
,那么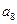 等于
等于