题目内容
(本小题满分l4分)如图,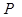 是抛物线
是抛物线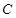 :
: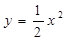 上横坐标大于零的一点,直线
上横坐标大于零的一点,直线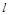 过点
过点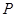 并与抛物线
并与抛物线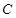 在点
在点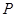 处的切线垂直,直线
处的切线垂直,直线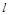 与抛物线
与抛物线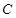 相交于另一点
相交于另一点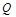 .
.
(1)当点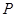 的横坐标为2时,求直线
的横坐标为2时,求直线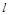 的方程;
的方程;
(2)若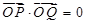 ,求过点
,求过点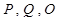 的圆的方程.
的圆的方程.
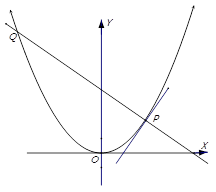
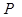 是抛物线
是抛物线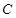 :
: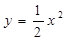 上横坐标大于零的一点,直线
上横坐标大于零的一点,直线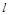 过点
过点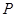 并与抛物线
并与抛物线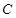 在点
在点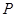 处的切线垂直,直线
处的切线垂直,直线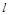 与抛物线
与抛物线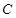 相交于另一点
相交于另一点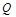 .
.(1)当点
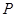 的横坐标为2时,求直线
的横坐标为2时,求直线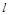 的方程;
的方程;(2)若
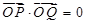 ,求过点
,求过点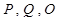 的圆的方程.
的圆的方程.
解:(Ⅰ)把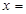 2代入
2代入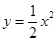 ,得
,得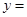 2,
2,
∴点坐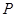 标为(2,2). ……………………1分
标为(2,2). ……………………1分
由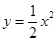 , ① 得
, ① 得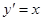
 ,
,
∴过点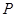 的切线的斜率
的切线的斜率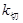
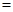 2,……………………2分
2,……………………2分
直线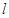 的斜率
的斜率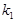
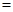
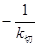
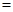
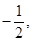 ……………………3分
……………………3分
∴直线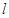 的方程为
的方程为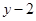
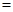
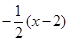 , 即
, 即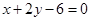 ……………………4分
……………………4分
(Ⅱ)设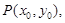 则
则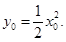
∵ 过点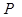 的切线斜率
的切线斜率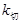
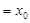 ,因为
,因为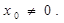
∴ 直线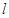 的斜率
的斜率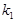
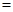
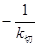
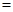
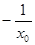 ,
,
直线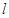 的方程为
的方程为 
 ②……………………5分
②……………………5分
设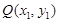 ,且
,且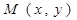 为
为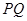 的中点,
的中点,
因为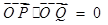 ,所以过点
,所以过点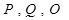 的圆的圆心为
的圆的圆心为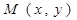
半径为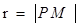 ,……………………6分
,……………………6分
且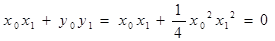 ,……………………8分
,……………………8分
所以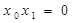 (舍去)或
(舍去)或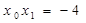 ……………………9分
……………………9分
联立①②消去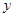 ,得
,得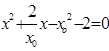 由题意知
由题意知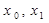 为方程的两根,
为方程的两根,
所以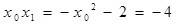 ,又因为
,又因为 , 所以
, 所以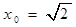 ,
,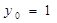 ;
;
所以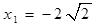 ,
,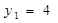 ……………………11分
……………………11分
∵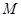 是
是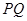 的中点,∴
的中点,∴ ……………………12分
……………………12分
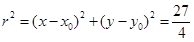
 ……………………13分
……………………13分
所以过点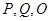 的圆的方程的方程为
的圆的方程的方程为
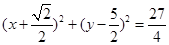 ……………………14分
……………………14分
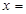 2代入
2代入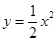 ,得
,得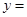 2,
2,∴点坐
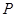 标为(2,2). ……………………1分
标为(2,2). ……………………1分由
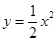 , ① 得
, ① 得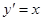
 ,
,∴过点
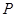 的切线的斜率
的切线的斜率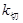
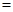 2,……………………2分
2,……………………2分直线
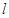 的斜率
的斜率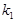
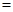
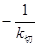
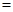
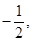 ……………………3分
……………………3分∴直线
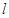 的方程为
的方程为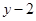
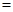
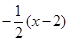 , 即
, 即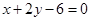 ……………………4分
……………………4分(Ⅱ)设
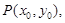 则
则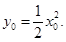
∵ 过点
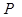 的切线斜率
的切线斜率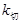
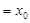 ,因为
,因为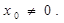
∴ 直线
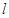 的斜率
的斜率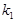
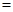
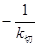
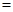
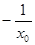 ,
,直线
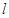 的方程为
的方程为 
 ②……………………5分
②……………………5分设
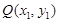 ,且
,且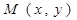 为
为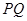 的中点,
的中点,因为
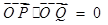 ,所以过点
,所以过点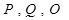 的圆的圆心为
的圆的圆心为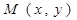
半径为
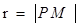 ,……………………6分
,……………………6分且
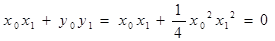 ,……………………8分
,……………………8分所以
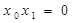 (舍去)或
(舍去)或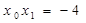 ……………………9分
……………………9分联立①②消去
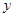 ,得
,得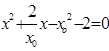 由题意知
由题意知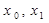 为方程的两根,
为方程的两根,所以
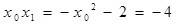 ,又因为
,又因为 , 所以
, 所以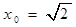 ,
,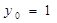 ;
;所以
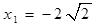 ,
,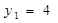 ……………………11分
……………………11分∵
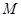 是
是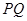 的中点,∴
的中点,∴ ……………………12分
……………………12分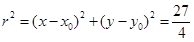
 ……………………13分
……………………13分所以过点
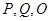 的圆的方程的方程为
的圆的方程的方程为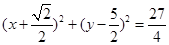 ……………………14分
……………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上一点到准线和抛物线的对称轴距离分别为10和6,则该点横坐标为
上一点到准线和抛物线的对称轴距离分别为10和6,则该点横坐标为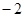 )的抛物线的标准方程为( )
)的抛物线的标准方程为( )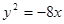
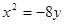
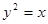 或
或
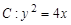 的焦点为
的焦点为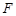 ,准线为
,准线为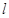 ,过抛物线
,过抛物线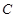 上的点
上的点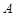 作准线
作准线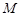 ,若
,若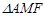 与
与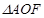 (其中
(其中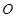 为坐标原点)的面积之比为
为坐标原点)的面积之比为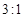 ,则点
,则点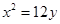 的焦点与双曲线
的焦点与双曲线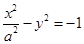 的一个焦点重合,则以此抛物线的焦点为圆心,双曲线的离心率为半径的圆的方程是___________。
的一个焦点重合,则以此抛物线的焦点为圆心,双曲线的离心率为半径的圆的方程是___________。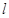 过抛物线
过抛物线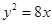 的焦点
的焦点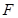 ,且与抛物线交于
,且与抛物线交于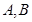 两点,若线段
两点,若线段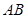 的中点到
的中点到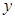 轴的距离是
轴的距离是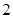 ,则
,则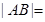 __ ▲ __.
__ ▲ __.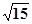 ,求抛物线的方程.
,求抛物线的方程.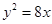 的焦点到准线的距离是( )
的焦点到准线的距离是( ) 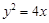 的焦点坐标是 .
的焦点坐标是 .