题目内容
6．已知tanα=4，则$\frac{{1+cos2α+8{{sin}^2}α}}{sin2α}$的值为（ ）| A． | 18 | B． | $\frac{1}{4}$ | C． | 16 | D． | $\frac{65}{4}$ |
分析 原式分子利用二倍角的余弦函数公式化简，再利用同角三角函数间基本关系变形，将已知等式代入计算即可求出值．
解答 解：∵tanα=4，
∴原式=$\frac{2co{s}^{2}α+8si{n}^{2}α}{2sinαcosα}$=$\frac{1+4ta{n}^{2}α}{tanα}$=$\frac{1+64}{4}$=$\frac{65}{4}$，
故选：D．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
1．不论m取何值，直线mx-y+2m+1=0恒过定点（ ）
| A． | $（1，\frac{1}{2}）$ | B． | （-2，1） | C． | （2，-1） | D． | $（-1，-\frac{1}{2}）$ |
18．若向量$\overrightarrow{AB}$=（-2，-3），$\overrightarrow{AC}$=（-4，-7），则$\overrightarrow{BC}$=（ ）
| A． | （-2，-4） | B． | （2，4） | C． | （6，10） | D． | （-6，-10） |
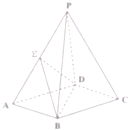如图，在四棱锥P-ABCD中，底面ABCD是矩形，E是棱PA的中点，PD⊥BC，求证：