题目内容
6.设直线ax+2y+6=0与圆C:x2+y2-2x+4y+1=0相交于点P,Q两点,CP⊥CQ,则实数a的值为( )| A. | 1 | B. | 2 | C. | 1或2 | D. | 3 |
分析 根据圆的标准方程,求出圆心和半径,根据点到直线的距离公式即可得到结论.
解答 解:圆的标准方程为(x-1)2+(y+2)2=4,圆心C(1,-2),半径r=2,
∵AC⊥BC,
∴圆心C到直线AB的距离d=$\sqrt{2}$,
即d=$\frac{|a-4+6|}{\sqrt{{a}^{2}+4}}$=$\sqrt{2}$,
解得a=2,
故选:B.
点评 本题主要考查点到直线的距离公式的应用,利用条件求出圆心和半径,结合距离公式是解决本题的关键.

练习册系列答案
相关题目
18.已知函数f(x)=$\frac{{e}^{x}}{x}$,则x>0时,f(x)( )
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值,又有极小值 | D. | 既无极大值也无极小值 |
14.已知函数f(x)=2sin(x+φ)(0<φ<π)是偶函数,则2cos(2φ+$\frac{π}{3}$)等于( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | $\sqrt{3}$ | D. | 1 |
15.已知函数y=f(x)对于任意的$x∈(-\frac{π}{2},\frac{π}{2})$满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式不成立的是( )
| A. | $\sqrt{2}f(\frac{π}{3})<f(\frac{π}{4})$ | B. | $\sqrt{2}f(-\frac{π}{3})<f(-\frac{π}{4})$ | C. | $f(0)<\sqrt{2}f(\frac{π}{4})$ | D. | $f(0)<2f(\frac{π}{3})$ |
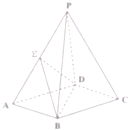 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证: