题目内容
10.求函数f(x)=$\frac{\sqrt{5-x}}{|x|-3}$的定义域.分析 由根式内部的代数式大于等于0,分式的分母不等于0联立不等式组求解x的取值集合得答案.
解答 解:由$\left\{\begin{array}{l}{5-x≥0}\\{|x|-3≠0}\end{array}\right.$,解得:x≤5且x≠±3.
∴函数f(x)=$\frac{\sqrt{5-x}}{|x|-3}$的定义域为{x|x≤5且x≠±3}.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
相关题目
2.在区间[-$\frac{3}{2}$,$\frac{3}{2}$]上随机取一个数x,使cos$\frac{π}{3}$x的值介于$\frac{1}{2}$到1之间的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
20.已知函数f(x)=2sin$\frac{x}{2}$的定义域为[a,b],值域为[-1,2],则b-a的值不可能是( )
| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{14π}{3}$ |
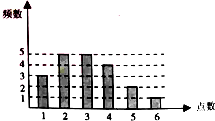 设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验.
设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验.