题目内容
19.在△ABC中,角 A,B,C所对的边分别为a,b,c,已知$b=\sqrt{3}a$.(1)当$C=\frac{π}{6}$,且△ABC的面积为$\sqrt{3}$时,求a的值;
(2)当$cosC=\frac{{\sqrt{3}}}{3}$时,求sin( B-A)的值.
分析 (1)由已知结合三角形面积公式即可求得a的值.
(2)由已知及余弦定理可得c=$\sqrt{2}a$,可得b2=a2+c2,由勾股定理可得B=90°,cosA=$\frac{c}{b}$=$\frac{\sqrt{6}}{3}$,利用诱导公式即可求得sin( B-A)的值.
解答 (本题满分为10分)
解:(1)∵$b=\sqrt{3}a$,△ABC的面积为$\sqrt{3}$,
∴S=$\frac{1}{2}absinC=\frac{\sqrt{3}}{4}{a}^{2}=\sqrt{3}$,
∴解得:a=2…4分
(2)∵$b=\sqrt{3}a$,$cosC=\frac{{\sqrt{3}}}{3}$,
∴由余弦定理可得:c=$\sqrt{2}a$,
∴b2=a2+c2,可得B=90°,
∴cosA=$\frac{c}{b}$=$\frac{\sqrt{6}}{3}$,
∴sin( B-A)=sin(90°-A)=cosA=$\frac{\sqrt{6}}{3}$…10分
点评 本题主要考查了三角形面积公式,余弦定理,勾股定理,诱导公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
9.用反证法证明某命题时,对结论“a、b、c、d中至少有三个是正数”正确的反设是( )
| A. | a、b、c、d中至多有三个是正数 | B. | a、b、c、d中至多有两个是正数 | ||
| C. | a、b、c、d都是正数 | D. | a、b、c、d都是负数 |
4.由直线y=0,x=e,y=2x及曲线$y=\frac{2}{x}$所围成的封闭的图形的面积为( )
| A. | 3+2ln2 | B. | 3 | C. | 2e2-3 | D. | e |
8.设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值所组成的集合为( )
| A. | [0,3] | B. | [0,4] | C. | [-1,3] | D. | [1,4] |
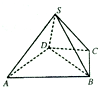 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.