题目内容
9．
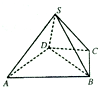如图，四棱锥S-ABCD中，△ABD是正三角形，CB=CD，SC⊥BD．（Ⅰ）求证：SB=SD；
（Ⅱ）若∠BCD=120°，M为棱SA的中点，求证：DM∥平面SBC．
分析 （Ⅰ）根据线面垂直以及线段的垂直平分线的性质证明即可；
（Ⅱ）由线线平行面面平行从而推出线面平行即可．
解答 证明：如图示：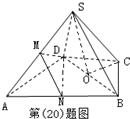
（Ⅰ）设BD中点为O，连接OC，OE，则由BC=CD知，CO⊥BD，
又已知SC⊥BD，SC⊥CO=C，所以BD⊥平面SOC，
所以BD⊥SO，即SO是BD的垂直平分线，所以SB=SD，
（Ⅱ）取AB中点N，连接DM，MN，DN，
∵M是SA的中点，∴MN∥BE，
∵△ABD是正三解形，∴DN⊥AB，
∵∠BCD=120°得∠CBD=30°，∴∠ABC=90°，即BC⊥AB，
所以ND∥BC，所以平面MND∥平面BSC，
故DM∥平面SBC．
点评 本题考查了线面、面面、线线平行的判定定理，考查看图能力，是一道中档题．
练习册系列答案
相关题目
17．函数f（x）=log2x+2x-6的零点一定位于下列哪个区间（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
14．下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y （吨）的4组对应数据：
若通过上表的4组数据，得到y关于x的线性回归方程为$\stackrel{∧}{y}$=0.7x+0.35，那么表中t的值应为2.8．
| x | 2 | 4 | 5 | 7 |
| y | 1.5 | t | 4.2 | 5.5 |